. Introduction
Speleothems are valuable archives of paleoenvironmental information. Their isotopic compositions of O and C and trace element contents, e.g., Mg, Sr, and Ba, are valuable sources of data on local conditions, such as the amount of precipitation or mean air temperature (Baker et al., 1993; Frisia et al., 2003; Roberts et al., 1998; Hu et al., 2008; Yuan et al., 2004; Wang et al., 2001, 2005; Fairchild and Baker, 2012). The additional advantage of speleothems is the fact that their age can be precisely estimated by the U-series method (Ivanovich and Harmon, 1992; Fairchild and Baker, 2012). Speleothem archives cover long periods of time and are usually one of the most continuous terrestrial archives. However, due to changing deposition conditions (e.g., temperature/humidity) or percolating water chemistry, breaks (hiatuses) in speleothem crystallization and erosional events are possible and relatively common (Fairchild and Baker, 2012).
According to Sadler (1981), sedimentation is essentially a discontinuous process. This is also true in the case of speleothems. Speleothems growth depend on specific conditions, such as the availability of water and its chemical composition, temperature, and CO2 pressure in the cave atmosphere, which must be lower than that in the dripping water so the degassing process can occur (Fairchild and Baker, 2012). In many cases, those requirements for speleothems crystallization are fulfilled only during the wet and/ or warm season of the year. Therefore, speleothems deposition occurs seasonally (Banner et al., 2007). However, seasonal sedimentation breaks are usually not detectable, and their duration is shorter than the resolution of the potential
paleoenvironmental records. Sedimentation breaks with durations longer than the resolution of the studied record (hiatuses) are an important problem in age-depth model construction, but they are themselves a source of additional and valuable climatic information. Their occurrence can relate to environmental changes such as turning into colder/ dryer climates or very local conditions such as changes in seepage water systems. The potential missing time hidden inside the hiatus is not only the duration of the potential break in sedimentation but also the time connected with potentially eroded strata.
The estimated age scale (chronology) for speleothems should consider the occurrence of the hiatuses. The most classic way to do that, commonly used in published works, is the dating of speleothem layers just below and above the hiatus visible in macro- or microscopic images and the calculation of the duration of the missing part of the profile based on the time difference between those two ages (Fankhauser et al., 2016; Steponaitis et al., 2015). However, this approach does not consider the fact that the sampled points are usually not placed directly on the hiatus borders. Therefore, the estimated hiatus duration includes, in addition to the deposition break duration and the part of the potentially eroded record, time recorded in the part of the profile between the dated points and hiatus. The more reliable solution is independent construction of age-depth models for parts of speleothems separated by hiatuses and the hiatus duration estimation based on the modeled ages of the hiatus borders (Lauritzen, 1995; Holzkamper et al., 2005; Vaks et al., 2006; Spötl and Mangini, 2007; Couchoud et al., 2009; Vansteenberge et al., 2016). This solution requires several reliable dating results or other time benchmarks for every continuous deposition phase. In some cases, such as a small thickness of the deposition phase or low quality of the speleothem material (e.g., high contamination by thorium (Th) and uranium (U) from the noncarbonate fraction or high porosity), it is not possible to obtain enough dating results for reliable age-depth model estimation (Jo et al., 2011). In such situations, the classic age-depth model approach cannot be used, and part of the stalagmite is left without precise chronology (see Jo et al., 2011). However, the problem can be solved by using other potential sources of chronological information.
Here, we present several examples of speleothem records with clearly visible hiatuses and possible methods of estimating the durations of the hiatuses. The first and the simplest example is the PD-4 stalagmite (Demänovská Cave System, Slovakia), where the hiatus duration can be estimated based on the classic age-depth modeling approach. The second example, the SC-3 stalagmite (Szczelina Chochołowska Cave, Tatra Mts., Poland), represents the situation where the alternative approach - oxygen isotopic stratigraphy (OIS) - is used to obtain additional chronological information for the part of the stalagmite located between hiatuses and where only one U-series age is available. Finally, the OIS and age-depth modeling approaches were tested on previously published data from Spain, Macedonia and South Korea. The last example is the flowstone profile in Ledena Dvorana (LDH; Snežna Cave, Slovenia). The LDH profile is divided by ten principal hiatuses. Its chronology is based on a set of paleomagnetic benchmarks. However, their number is too low for the estimation of age-depth models for every deposition phase by classic age-depth modeling. This profile is an example of how the chronology of the whole profile can be estimated based on OIS and independent age benchmarks.
. Material and Local Settings
PD-4 stalagmite
The PD-4 stalagmite was collected in the Demänovský jaskynný systém (Demänová Cave System, DCS). The DCS is situated in the Nízke Tatry (Low Tatra) Mountains (Western Carpathians, Slovakia; 19.58° E 49° N; the entrance elevation is 812 and 837 m.a.s.l; Fig. 1A). The total length of the DCS corridors is approximately 41.4 km (Herich, 2017). The PD-4 sample was taken in the Pekelný Dóm Chamber, located at the lower level of the DSC with the active underground stream of the Demänovka Stream. PD-4 is an approximately 385-mm-long calcite stalagmite of light cream color. The stalagmite is divided into two parts by a layer of sand cemented by calcite. This layer documents the break in calcite crystallization and filling of the cave passage by sand. The part of the stalagmite below the sand layer is 96 mm long. The calcite here is laminated and has several macroscopically visible pores. These pores do not contain any detrital particles or younger crystallization traces. The part of the stalagmite above the sand layer is 290 mm long, and it has lamination, color and porosity similar to that of the lower part (Fig. 1C).
SC-3 stalagmite
The SC-3 stalagmite has been collected in Szczelina Chochołowska Cave in Tatra Mts (Błaszczyk et al., 2020). The SC-3 stalagmite is approximately 240 mm long and contains four phases of continuous growth separated by three discontinuities. These growth interruptions are underlined with layers of detrital material (Fig. 1D) and was identified at 186 mm (H-1), 196.6 mm (H-2) and 230 mm (H-3) from the base of the stalagmite (Błaszczyk et al., 2020).
Ledena Dvorana flowstone profile
Snežna Jama (Ice Cave) is located on the southeastern slope of Raduha Mountain in the northeastern part of the Kamnik–Savinja nik– Alps (Kamniško–Savinjske Alpe, NW Slovenia, 46°23’53”N, 14°44’31”E, 1514 m.a.s.l.; Fig. 1A). The speleothem profile is situated in the Ledena Dvorana (Ice Hall – LDH), approximately 90 m from the cave entrance at a depth of approximately 45 m below the entrance. The speleothems were deposited as an approximately 2.4-m-thick complex sequence of flowstone (Fig. 1F). Numerous breaks in deposition (hiatuses) are expressed as more or less distinct horizontal, inclined or wavy bedding plains of different character and strength. Hierarchically, the most important breaks in the deposition of flowstones are characterized by the growth of stalagmites, corrosion surfaces, fissuration (e.g., 160 and 700 mm), and by the pseudo-oolithic bases of some overlying layers (e.g., 720 mm). Less important hiatuses are mostly expressed as single bedding plain disconformities. The stalagmites grew during several different periods, especially in the upper half of the profile (above approximately 155 cm). They were completely buried by younger sequences of flowstone. Some of them were broken off approximately at the level of the next distinct hiatus. Judging from their length (mostly up to 500 mm; Bosák et al., 2002), it is believed that their growth required only a few tens of ka. The LDH profile drawing and scheme of unconformities (Bosák et al., 2002; Zupan Hajna et al., 2008; Häuselmann et al., 2015) were originally correlated with speleothem slabs cut from the profile and used for stable isotope study.
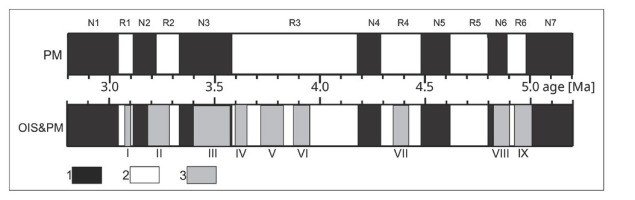
The high-resolution paleomagnetic (PM) analysis (Bosák et al., 2002) identified a complex magnetostrati-graphic profile (Fig. 1E) with an alternation of seven normal (N)-polarized and six reverse (R)-polarized magnetozones. Detailed paleomagnetic study of the profile shows some magnetozone borders (at 163.7 or 1530 mm) are located at the deposition breaks (in Table 2 marked as italic). Obtained magnetozone scheme was correlated with the GPTS (Ogg, 2012) and was interpreted successively by Bosák et al., (2002), Zupan Hajna et al., (2008), and finally by Häuselmann et al., (2015). Authors stressed the correlation problems caused by partial erosion of the flowstone sequence. The succession, boundary depths and ages of the magnetozones are summarized in Table 2. The magnetozones are numbered from the top to the base. Their boundaries (PM benchmarks) are marked by numbered N/R or R/N symbols. Each benchmark is characterized by two parameters: (a) the depth with errors resulting from the field measurements (using wooden or tape measures) and (b) boundary ages (according to Ogg, 2012) with assumed uncertainty of 1.5%.
U-series analyses of several samples collected from the profile proof the age of flowstone sequence is out of U-Th method range. The previous measurements of uranium concentration in the set of samples from the LDH profile gave results in the range from 0.02 ppm to 0.07 ppm (Häuselmann et al., 2015), far too low for applying uranium–lead chronology.
. Methods
U-series dating
Calcite samples were drilled along the profiles of the studied speleothems. The mass of the collected samples was in the range of 0.1–0.5 g. The thicknesses of the sampled layers were up to 2 - 4 mm. Chemical treatment was performed at the U-series Laboratory of the Institute of Geological Sciences, Polish Academy of Sciences (Warsaw, Poland). First, the samples were treated at high temperature (800°C, over 6 h) for decomposition of the organic matter. The isotopic spike (233U, 236U, 229Th) was added to the samples before the chemical procedure. The samples were dissolved in nitric acid, and uranium and thorium were separated from the carbonate matrix by the chromatographic method using TRU Resin (Hellstrom, 2003). Internal standards and blank samples were treated by the same procedure as that of all the studied samples. The measurements of U and Th isotopic compositions of all samples and standards were performed at the Institute of Geology of the Czech Academy of Sciences (Prague, Czech Republic) by a double-focusing sector-field ICP mass analyzer (Element 2, Thermo Finnigan MAT). The instrument was set on a low mass resolution (m/Δm≥300).
The measurements were corrected for background counts and chemical blanks and reported as the activity ratios. U-series ages were calculated based on measured 230Th/234U and 234U/238U activity ratios using the newest decay constants (in yr-1): λ238=(1.55125±0.0017).10- 10 (Jaffey et al., 1971), λ234=(2.826±0.0056).10-6 (Cheng et al., 2013), λ232=(4.95±0.035).10-11 (Holden, 1990), and λ230=(9.1577±0.028).10-6 (Cheng et al., 2013). The age errors were calculated by considering all uncertainties, except the decay constant, using error propagation rules.
Oxygen isotope analyses
Samples for δ18O analyses were taken along the growth axes of the speleothems by drilling. The analyses were carried out at the Stable Isotope Laboratory, Institute of Geological Sciences, Polish Academy of Sciences, Warsaw. Oxygen stable isotopic composition was determined using a Thermo KIEL IV Carbonate Device coupled with the Finnigan Delta Plus IRMS spectrometer in a dual inlet system. The COfrom the calcite was extract-2 ed using orthophosphoric acid (density 1.94 g.dm-3) at 70°C. International standard NBS 19 was analyzed with every ten samples. The isotope ratios obtained are reported as delta (δ) values and expressed relative to the V-PDB standard. The measurement precision (1 standard deviation) is 0.10‰ for δ18O.
Age-depth model construction
Based on the obtained U-series dating results, an age-depth model was created using the MOD-AGE algorithm (Hercman and Pawlak, 2012). First, the ages included in the model were calculated based on the corrected values of activity ratios. The depth values were described as normal distributions. Age-depth relationships were estimated using the locally weighted scatterplot smoothing (LOESS) technique (Cleveland, 1979). The chosen span value for the LOESS model was the highest value of span, which allowed the estimation of an age-depth model corresponding to all data points inside the 2σ error band (Hercman and Pawlak, 2012).
Oxygen isotope stratigraphy
Oxygen isotopic stratigraphy (OIS) is based on the assumption that changes in the δ18O of speleothems have a regional or global nature. Therefore, it is possible to correlate the δ18O record with the reference (global or regional) δ18O record. The potential reference record should have a well-established age scale and high resolution, and it should record environmental changes similar to those of the correlated record. This means that oxygen isotopic composition changes recorded in the studied speleothem record and reference curve should be coincident and controlled by the same factors. Therefore, the correlation should provide additional chronological information. The choice of the proper reference record is crucial here. Long-term marine records or ice core records can be useful as reference records due to their overall regional nature and well-defined time scale (Lisiecki and Raymo, 2005). The speleothem oxygen stable isotope (δ18O) records require data standardization before correlation with the marine record. Records from different environments may have different amplitudes and mean values. The correlation process uses relative changes in the isotope composition, not absolute values. The δ18O records from different regions and the archives of different types may express the same climate changes but with different amplitudes and mean values. To avoid the potential threats of amplitude differences, the oxygen isotopic records were normalized. We used the same time window to determine the normalized values for the correlated and reference records. There was one mean value determined for all parts separated by hiatuses in the δ18O record from the selected speleothem.
The next problem is the different reactions of caves and oceans to global changes induced by the same factors. During glaciations, for instance, ocean water becomes enriched in heavier oxygen isotopes, while meteoric water is enriched in light oxygen isotopes. For the speleothem records, the δ18O composition of meteoric water is one of the dominant factors. Therefore, we can expect that signals in the speleothem records will have a negative correlation with the marine signals. To solve this problem, in the case of correlation with marine records, we inverted our speleo-them δ18O records for intercorrelation purposes.
The correlation was performed with GenCorr software (Pawlak and Hercman, 2016). GenCorr seeks an optimal correlation (greatest similarity) between two or more isotopic records by using several correlation procedures. The basic procedure assumes no knowledge of the ages of the record and thus attempts their correlation in a completely free mode. The next step requires some knowledge of the likely ages and uses it in correlation. Age information in the form of age-depth models can be put into GenCorr, allowing the procedure to find the optimal fit for two or more records within the limits of the model confidence bands. However, it is not always possible to make continuous age-depth models for every profile. In the most typical situation, only some information about the correlated age records is available, such as a few dating results or knowledge of the likely age limits/boundaries. This type of information may be used for chronological benchmarks in the correlation process. Two types of benchmarks are possible: (i) fixed benchmarks where there is no information about their age uncertainty, and (ii) age information having normal, uniform or skewed distribution (e.g., dating results). The age assigned for a fixed benchmark remains constant during the entire correlation procedure, while ages assigned for nonfixed benchmarks may change according to their distribution. In both cases, the ages assigned for the points between the benchmarks are calculated in a random way. The only assumption here is that the ages assigned for points between the benchmarks have to be in accordance with the ages assigned for the benchmarks and their stratigraphic positions.
The GenCorr correlation was run with a population of 9,000 individual solutions. Each solution represents one possible position for a matched record on a basic reference time scale. The mean Euclidean distance between the records was used as a heuristic function for the genetic algorithm. The procedure was terminated after 320 algorithm cycles, when further improvements in the optimization became insignificant in scale (Pawlak and Hercman, 2016).
The confidence band estimated for the correlation results considers the uncertainty of the reference curve and the alignment uncertainty. At the initial stage of the population creation, a Monte Carlo method is used to randomize the age of the points from the reference curve. Those points are randomized from a normal distribution, which describes their uncertainty, in the range of 2σ. In the next step, different individuals, of correlated record, are aligned to different individuals of reference curve. Finally, based on the population of results a confidence band for the correlation results can be estimated and it includes reference curve error and alignment error.
The reference records used for OIS correlation in described examples are the marine stack records and Greenland ice core records. Their chronology was built based on independent age benchmarks and orbital tuning of δ18O records (Lisicki and Raymo 2005). For the purpose of the correlation procedure, we assumed 2.5% error for the used reference records (Lisicki and Raymo 2005). The error of the whole correlation procedure result was estimated based on the Monte Carlo method, taking into account the reference and studied record errors, chronology benchmark errors and the correlation procedure error. The whole correlation procedure was repeated 40 times for every presented example. On the basis of the obtained set of results, the median (age-depth model) and its 2 σ error were estimated (Pawlak and Hercman, 2016).
Paleomagnetism
Paleomagnetic analyses were completed in the Department of Palaeomagnetism, Institute of Geology of the Czech Academy of Sciences, Průhonice (Czech Republic). Samples were demagnetized by alternating field (AF) and/ or demagnetized thermally (TD). The AF demagnetization was carried out up to a field of 100 mT in 12–16 steps. A MAVACS apparatus (Příhoda et al., 1989) was used for the TD. The natural remnant magnetization (NRM) was measured with a JR–6A spinner magnetometer (Jelínek, 1966) and/or a 2G superconducting rock magnetometer with an incorporated AF unit. The magnetic susceptibility (MS) values were measured on KLY–2 (or KLY–3) kappa bridges and a KLF–4A automatic magnetic susceptibility meter (Jelínek, 1966, Jelínek, 1973). The multicomponent analysis technique of Kirschvink (1980) was applied to separate individual NRM components. The characteristic component (high field and/or high temperature) is stable and can be isolated in the AF and/or TD (approximately 15–80 mT, 350–540°C). Fisher statistics (1953) were employed for the calculation of the mean directions of the NRM components derived by the multicomponent analysis. The flowstones are characterized by very low to high NRM and MS values. The NRM intensities are between 0.2 and 523 mA.m-1, and the MS values are between -13 and 324 SI units. Applied PM methods, data interpretation and correlations were presented by Zupan Hajna et al., (2008), and a summary and synthesis of the results were presented by Häuselmann et al., (2015).
. Results
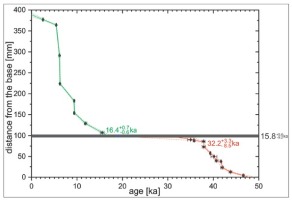
Classic approach U-series dating and age-depth modeling (PD-4 stalagmite)
The results of U-series dating of the PD-4 stalagmite are presented in Table 1. The reported errors represent 2 standard deviations. Based on U-series ages, two age-depth models for continuously deposited parts of the stalagmite have been constructed. The model for the older part was calculated based on 11 U-series ages (Fig. 2). According to the model, stalagmite growth started at
Table 1
U-series dating results for the SC-3 and PD-4 stalagmites.
U-series and age-depth modeling combined with oxygen isotope stratigraphy (SC-3 stalagmite)
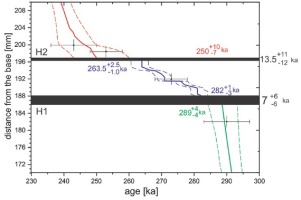
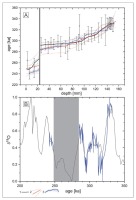
A series of fifteen U-series ages were obtained from the whole stalagmite (Błaszczyk et al 2020). In our study, we have used only dates located close to H1 and H2 hiatuses (Table 1). The reported errors represent 2 standard deviations. Only one U-series data point, 273 ± 5 ka, was obtained for the layer between the hiatuses (H2 and H1 on Fig. 3). Based on one U-series age, it is not possible to estimate the age-depth model for this part of the stalagmite. The older and younger parts of the studied stalagmite have well-defined age-depth models estimated by MOD-AGE software. The age range of this deposition phases is 327±7 ka and 289±4 ka for the older phase and
Fig 3
Age-depth models for the SC-3 stalagmite with the estimated durations of the hiatuses H1 and H2: A – the age-depth model chart of the whole profile; B– enlarged H1 and H2 zones; age-depth model for the oldest deposition phase (green lines); age-depth model for the deposition phase between H1 and H2 (blue lines); and age-depth model for the youngest deposition phase (red lines).
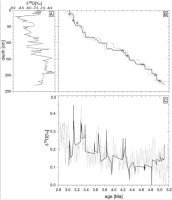
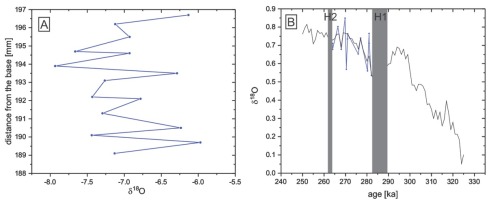
For the part of the stalagmite between hiatuses, an age-depth relation was constructed using the OIS approach using the LR04 combined record (Lisiecki and Raymo, 2005) as a reference curve. The set of fifteen samples for δ18O analyses was collected from this part of the stalagmite located between the H1 and H2 hiatuses (188–196.5 mm; Fig. 4A) at a resolution of one sample per 0.5 mm. The value of δ18O varies in the range of 1.8‰ (from -7.8‰ to -6‰). Three age benchmarks have been used. The first is the U-series dating result obtained for this part of the stalagmite (Table 1) as an independent age benchmark with a normal distribution. The other two benchmarks are border ages from age-depth models of the parts below the H1 hiatus and above the H2 hiatus. The OIS (Fig. 4B) places the deposition of the stalagmite parts located between the hiatuses in the age range between
Fig 4
The δ18O data for the SC-3 profile: A – the δ18O record in the depth scale; B – the result of the correlation with the LR04 record.
Based on the three independent age-depth models, it is possible to estimate the time duration of the H1 and H2 hiatuses. The H1 hiatus covers the time between 289±4 and
Paleomagnetism (PM) combined with oxygen isotope stratigraphy (OIS) – (Ledena Dvorana – LDH profile)
The LDH δ18O record in its depth scale is presented in -6.5‰. The record has a clearly visible depleting trend from the 200-cm mark (bottom of the profile) to the top 20 cm. The youngest 20 cm of the record is characterized by a rapid increase from -9.5‰ to -7.5‰ δ18O. Apart from these trends, the record contains thirteen cyclic changes with amplitudes of approximately 1‰. The LDH section contains several visible breaks in deposition, seen as thick lines in Fig. 6. Three of the magnetozone borders are located at the hiatuses. It must be assumed that part of those magnetozones must be not deposited or eroded. These age benchmarks (magnetozone boundaries) cannot be used for chronology construction and duration estimation of deposition breaks. Therefore, for the purpose of chronology construction, we use only those PM benchmarks that are located inside the episodes of continuous deposition phases.
Fig 6
LDH profile: A – sketch of the LDH profile with sampled sections (rectangles) and principal hiatuses (lines); B – the result of OIS and the PM age-depth modeling, with detected hiatuses and their duration (gray rectangles). Arrows show the relation between the hiatuses visible in the profile and the hiatuses detected by the model.
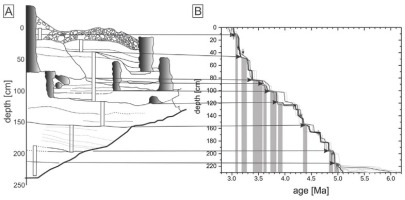
The combination of the PM information and the OIS approach (OIS+PM) allows GenCorr (Pawlak and Hercman, 2016) to search for optimal positions within the time intervals defined by the PM benchmarks (Fig. 5C; black line). The OIS+PM correlation places the LDH profile between 2.95 and 5.1 Ma (Fig. 5C; black line). With this solution, the LDH δ18O record is in good agreement with the principal trend in the LR04 δ18O record, and the major peaks in the two records are also well correlated (Fig. 5C; black line).
The OIS+PM age-depth model suggests nine hiatuses (Fig. 6B). These hiatuses are in good agreement with the principal hiatuses observed in the LDH profile (Fig. 6A; thick lines). The gray rectangles in Fig. 6B show the suggested duration of those hiatuses.
. Discussion
The estimation of hiatus duration is a common geological problem. In fact, based on the chronological information only, it is not possible to estimate the hiatus duration, which is understood as a non-deposition time. The calculated time is rather a sum of “non-deposition time” plus the time recorded in potentially eroded strata. The time missed in the hiatus can be estimated by the calculation
of two independent age-depth models for the parts of the profile below and above the hiatus. This method is commonly used in speleothem science (Lauritzen, 1995; Holzkamper et al., 2005; Vaks et al., 2006; Spötl and Mangini, 2007; Couchoud et al., 2009; Vansteenberge et al., 2016). The classic age-depth modeling approach on data from the PD-4 stalagmite allows us to estimate the hiatus duration (Fig. 2) as 15.8 ka. It is the time of a break in calcite deposition and possible erosion of the older part of the stalagmite. At this time, caves were flooded a minimum of two times and sand deposition occurred. U-series data of 19±0.2 ka were obtained for samples taken from the thin calcite layer (Fig. 1C) inside the sand, observed only in the axial part of the stalagmite, documenting a short episode of calcite crystallization just after the LGM.
However, in some cases, it is not possible to estimate a reliable age-depth model for continuously deposited parts of the speleothem. First, the quality of the calcite material, for example, strong detrital contamination or extremely low uranium content, may prevent reliable isotope dating results. Second, the studied speleothem age may be beyond the range of the dating method. In such cases, we have limited age information available. Sometimes, obtaining any chronological information is extremely important due to the importance of the paleoenvironmental record preserved in the studied speleothem. The only solutions for obtaining some chronological information are using relative or non-isotopic methods, for example, paleomagnetism, bioindicators, or isotopic stratigraphy. Commonly used paleoclimatic proxies in speleothem science are changes in oxygen isotopic composition. This creates opportunities for using the correlation of the oxygen isotopic record from the studied speleothem with the global/regional reference oxygen curve (OIS approach).
However, the OIS approach presents a few important problems that must be solved. First is the selection of the proper reference curve. The use of marine stack records such as LR04 is common and reliable when we can assume that the correlated δ18O record reflects over regional changes. Isotopic changes in the studied record and reference curve must be coincident (in the confidence bands of the records) and controlled by the same factors. The main factors shaping the δ18O speleothem records during the last 200 ka in Europe is temperature (Różański et al., 1993; Moseley et al., 2015; Kern et al., 2019; Comas-Bru et al., 2020) and δ18O composition of precipitation, source effect. The Atlantic Ocean is the main source of moisture for precipitation on the European continent (McDermott et al., 2011). The LR04 is a foraminifera benthic stack record, basing on 57 globally distributed sites. The benthic stack record reflects the variability in δ18O of global nature, and it is driven mostly by changes in the global ice volume. The δ18O speleothem records, driven mostly by source effect and temperature effect, can also reflect long time changes of global nature. Therefore, they can be correlated with LR04 stack record if the global signal is not biased by the influence of regional or local effects. There are differences in the local stacks from Atlantic and Pacific Oceans (Lisiecki and Stern, 2016). The Atlantic regional stacks, which resemble LR04 during MIS 5, display a more gradual transition than the Pacific stacks during glacial–interglacial transitions like MIS 5e/5d. Additionally, there is ca. 0.7 ka bias observed between stack records from Indian and Pacific Oceans. However, majority of the records from LR04 stack (40 sites) is located on Atlantic Ocean (Lisiecki and Raymo, 2005). Therefore, LR04 stack is biased toward Atlantic stack records and is suitable for correlation with European speleothems. When there is more than one potentially available reference curve, running test correlations with all available reference records is recommended, and those that give the better correlation quality indicator are chosen. In the study of RP-66 flowstone from the Reciska Pecina Cave (Hercman et al., submitted) in Slovenia, three potential reference curves were considered: LR04 (Lisiecki and Raymo, 2005), the stack of oxygen isotope records for Mediterranean Sea sediments (Wang et al., 2010), and the PISO record (Channell et al., 2009). Sixty test correlations were performed for each of those reference curves. The results unambiguously show that the correlations with the MEDI record have the best correlation quality results (Fig. 7) and used for detailed study.
Fig 7
The results of testing reference curves: A – quality indicators for the series of test correlations with different reference curves; B – Reciska Pecina curve correlated with the MEDI curve (Wang et al. 2010); C – Reciska Pecina curve correlated with the LR04 curve (Lisiecki & Raymo 2005); D – Reciska Pecina curve correlated with the PISO curve (Channell et al. 2009).

Next, the reference curve and the studied record should be characterized by similar resolution.
Lower resolution causes the loss of recorded information, which makes correlation more difficult. The results of the published tests (Pawlak and Hercman, 2016) show that when the distance between data points becomes larger than the signal period in the record, it causes a large decrease in the correlation quality (Pawlak and Hercman, 2016). The use of OIS for profiles with hiatuses requires a preliminary test of the method used to correlate sensitivity to the lack of part of the record in the correlated profile (breaks in deposition) and how it can influence the normalization procedure, especially if the local extremum is missing in the hiatus part. During initial work with the correlation procedure, we performed a set of tests to determine how the potential hiatus influences the whole correlation procedure, including normalization (Pawlak and Hercman, 2016). The results show that the whole procedure can be robust until the hiatus is no longer than approximately 15% of the whole correlated record length.
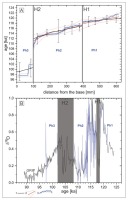
The Macedonian stalagmite OH2 (Regattieri et al., 2018) chronology is based on U-series ages (Fig. 8). The U-series ages for this stalagmite have approximately 20 ka large uncertainties, and they are not in proper order (Fig. 8). Therefore, the age-depth models estimated by StalAge (in original paper) and calculated here by MOD-AGE have large error bands. We correlated the δ18O records from this stalagmite with the stack of oxygen isotope records for Mediterranean Sea sediments (MEDI; Wang et al., 2010). From the previous works in a Mediterranean basin, we know that the δ18O records from stalagmites reflect the changes in Mediterranean Sea isotopic composition (Ayalon et al., 2002). The age-depth model obtained by OIS correlation agrees with the age-depth models based on U-series ages. The obtained confidence band varies from ca. 4 to 10 ka. Those differences reflect the quality of correlation for different parts of the correlated records. Intervals with wider confidence bands have larger alignment error, and it reflects the fact that single pick on correlated record can be aligned to reference curve in a different way with similar correlation quality.
Fig 8
The comparison of age-depth models for stalagmites from an unsurveyed Macedonian cave located near Lake Ohrid (Regattieri et al. 2018): A – the results of age-depth model estimation – (1) age-depth model made by the authors; (2) age-depth model made by MOD-AGE; (3) age-depth model made by the OIS approach; B – the result of the correlation with the MEDI record (Wang et al. 2010).
The correlation of the older part is reliable, and the shape of the OH2 δ18O records agrees with the MEDI record and has a better position than its original chronology (Fig. 8). Therefore, the OIS information potentially improves the existing chronology if the assumption about the synchronicity of the records is met. The correlation for the δ18O record from the younger part of the stalagmite is more problematic. The GenCorr software correlates only the main trend of the OH2 record here, and the short time pick does not meet its analog on the MEDI curve in this position.
The thin layers located between the two hiatuses may not have enough U-series ages or other independent age benchmarks for age-depth model construction (e.g., Jo et al., 2011, Błaszczyk et al., 2020). In the case of the SC-3 stalagmite, there are three continuous episodes of calcite deposition separated by the two hiatuses. The oldest and the youngest growth phases have sets of reliable U-series ages. Therefore, the classic age-depth modeling approach has been used for the estimation of age borders for the oldest and the youngest crystallization phases (Błaszczyk et al., 2020). The problem is the thin (approximately 10 mm thick) crystallization phase between the hiatuses H1 and H2, where only one reliable U-series age was obtained. The OIS application allows us to estimate the age-depth model between the H1 and H2 hiatuses and estimate their duration as 7±6 and
Fig 9
The result of correlation of the DY-1 δ18O record with the LR04 record: A – the δ18O record correlated with LR04; B – age-depth model estimated for phase B (blue lines) and age-depth models estimated for phases A and C based on the U-series ages (data from Jo et al. 2011) – (1) LR04 record; (2) DY-1 δ18O record; (3) age-depth model made by the authors (Jo et al. 2011); (4) age-depth model made by the OIS approach.

Fig 10
The comparison of age-depth models for stalagmites from Spanish Cobra Cave (Rossi et al. 2014): A – the results of age-depth model estimation – (1) age-depth model made by the authors, fluorescence lamina counting (Fl); (2) age-depth model made by MOD-AGE; (3) age-depth model made by the OIS approach; B – the result of the correlation with the GRIP record.
In the previous examples, we used U-series ages as the pointed age benchmarks, and every depositional episode had at least one defined age benchmark. The last example (LDH profile) is beyond the U-series age limits. Additionally, the uranium concentrations measured in a set of samples from this profile are lower than 0.07 ppm (Häuselmann et al., 2015). It is far too low for eventual application of U–Pb dating. The LDH profile chronology is based on eight paleomagnetic benchmarks (Table 2). The whole profile has ten principal hiatuses and eleven sedimentation phases. Therefore, the number of points with defined ages is far too low to estimate age-depth models for the individual sedimentation phases. In this case, due to the LDH profile age and its duration, the LR04 stack record is the only robust δ18O record available that covers the required interval.
Table 2
Position of magnetozones in the LDH profile.
[i] Explanations: N– normal polarity, R– reverse polarity; *after Ogg (2012); ** depth with error; *** age with assumed age uncertainty (for explanations, see the text). PM benchmarks marked as italic are located at hiatuses and were not included into PM+OIS chronology
One of the advantages of GenCorr software is the sensitivity for deposition breaks (see Pawlak & Hercman 2016). The OIS+PM chronology may be verified by comparisons of the locations of hiatuses derived from the correlation results with their actual positions in the LDH section (Fig. 6A). The whole LDH profile is correlated to the LR04 record with no assumption about continued/discontinued deposition (Fig. 5; black line). The OIS+PM age-depth model suggests nine hiatuses, all of which can be identified with breaks in the LDH lithological log (arrows between panels A and B in Fig. 6). However, within the LDH speleothem profile, the accuracy of the OIS chronology will depend primarily on the precision of the field measurements of PM sample position. These were mostly within 1–2 cm, with a maximum of 4 cm (Table 2). In general, we may state that unconformities/hiatuses detected by the combined OIS+PM chronology are in relatively good agreement with the lithological log.
A comparison of the ages estimated for the LDH with the GPTS records (Ogg 2012) shows that hiatuses can significantly distort magnetozone stratigraphic relationships, especially their thicknesses. This effect is particularly strong for zones N2 and N3 in the younger part of the LDH profile and for zones N6 and R6 in the older segments. The duration of breaks in deposition is much longer than that suggested by Bosák et al., (2002). The longest periods of non-deposition are detected inside the N3, R2, and R3 zones and cover time spans of approximately 185, 100 and 95 ka, respectively (Fig. 11).
Fig 11
The comparison of the GPTS record (Ogg 2012) with the time scale of the LDH section obtained by integrated OIS and PM chronology: 1 – normal polarity, 2 – reverse polarity, 3 – non-deposition time (hiatus).
. Conclusions
Deposition breaks in speleothems are often caused by climatic factors, so they are carriers of climatic information. Hence, the correct and possibly accurate estimation of the durations of breaks is important for accurate paleoclimatic reconstructions.
The approach based on two dated points located close to hiatus boundaries may not be precise enough to estimate the time hidden in the hiatus because dated points are never located directly on the hiatus boundaries. The age-depth modeling approach gives robust results. However, it is not always possible to have a sufficient number of age data to calculate independent age-depth models for individual depositional phases.
Our study shows different situations in several examples of speleothems with hiatuses: (1) stalagmite PD-4 (Slovakia), where the hiatus duration was estimated by the classic age-depth modeling approach based only on U-series data; (2) stalagmite SC-3 (Poland), where oxygen isotopic stratigraphy is used to establish the chronology in a part of the stalagmite with only one U-series age; and (3) the flowstone profile from Ledena Dvorana in Slovenia, where the chronology bases on paleomagnetic benchmarks and oxygen isotopic stratigraphy. Additionally, the three examples selected from the literature: (1) a stalagmite from Daeya Cave (Korea); (2) a stalagmite from Cobre Cave (Spain); and (3) one stalagmite from a Macedonian cave located near Lake Ohrid, were used. In the case of two examples, first from Cobra Cave and second from the Macedonian cave, the long δ18O record can have episodes when local conditions have a strong impact on its values, and this part of that record cannot be correlated to the reference curve. Therefore, the results of the OIS correlation should be verified by independent chronology, such as U-series ages. Nevertheless, the OIS approach combined with the independent chronological information, such as U-series ages, can be helpful for the detection of hiatuses and estimation of their duration. Finally, the flowstone profile of the Ledena Dvorana (LDH; Slovenia)-layered complex, divided by ten principal hiatuses, is an example of a profile where the OIS approach is the only reliable option for determining the chronology of all deposition phases. The obtained OIS age-depth model is in accordance with PM benchmarks and with hiatuses detected in the profile. Generally, the OIS correlation can be a useful tool for the estimation of duration of hiatuses and chronology of the speleothem profiles beyond the U-series age limits. Additionally, the OIS approach can be used for the improvement of the existing chronologies with a large error. The main threats for this approach are potential diachronicity of the reference curve and correlated record.