1. Introduction

Dating paleo-earthquake events is very important for estimating earthquake hazards. High-resolution and high-precision dating of seismic events that help to calculations of recurrence intervals on timescales of decades to several thousand years is challenging, particularly in semi-arid to arid settings, where organic debris for ¹⁴C dating is uncommon. Recent studies (e.g., Banerjee et al., 2001; Lu et al., 2007; Porat et al., 2009; Fattahi et al., 2010; Liu et al., 2010; Wang et al., 2012) have shown that optical dating of earthquake-related deposits is capable of producing robust chronologies of paleo-earthquake events. However, a potential problem in such settings is that light exposure of earthquake-related sediments may have been insufficient to fully reset (bleach) the OSL signal prior to deposition (Cunha et al., 2009; Yang et al., 2012).

Incomplete resetting of the OSL signal will lead to age overestimation. Fuchs et al. (2005) and Olley et al. (1998) examined the dependence of bleaching on grain size. It is now well known that quartz OSL signals bleach more easily than feldspar IRSL (infrared stimulated luminescence) signals (Yang et al., 2012), and in many cases it appears that coarse grain (74–250 μm) bleaches better than fine grain (4–11 μm) quartz (Yang et al., 2012). But in fact, samples from different depositional environments may have different bleaching characteristic.

The August 23, 1985 Ms7.1 Wuqia Earthquake ruptured the eastern segment of the seismically active Pamir Front Thrust at the leading northeastern edge of the Pamir salient of the Tibetan Plateau, producing a 15-km long surface fault scarps, and destroying the old Wuqia town (Feng et al., 1986). Data on the recurrence period of such devastating earthquakes is a vital input for seismic hazard evaluation and risk assessment in this region. In this study, we test one modern sample and three samples from a trench excavated across the 1985 Wuqia Earthquake surface rupture (Fig. 1) using a variety of techniques on fine grain quartz (FQ) and coarse grain quartz (CQ). The purpose is to test assumptions regarding the zeroing of the deposition after the Wuqia earthquake, to assess which grain sizes are most appropriate and which dating technique can provide reliable ages for earthquake related rapidly-deposited sediments. Finally we also applied time-saving protocols such as small aliquot standardised growth curve (SA-SGC) (Roberts and Duller, 2004; Lai et al., 2007, Li et al., 2015) to check its potential for dating heterogeneously reset samples.

Fig. 1

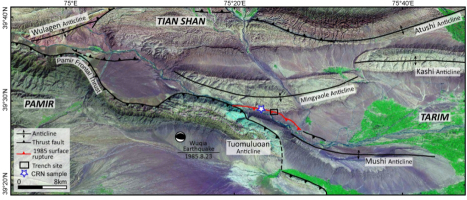
Aster image showing regional tectonic structure, the 1985 Wuqia earthquake surface rupture and trench location. Modified from Li et al. (2012).

2. Materials and methods

Samples and instruments

A trench (Fig. 2b) was excavated across a small sag pond of the 1985 Ms7.1 Wuqia Earthquake surface fault scarp at a fluvial terrace and exposed a sequence of slope deposited silts and sands mainly sourced from the Pliocene sandstone and siltstone rocks 200 m to the north (Fig. 1). Four earthquake events including the 1985 event were identified in the trench. Three samples deposited before the 1985 earthquake were collected from trench, and one sample deposited after the 1985 earthquake (Fig. 2 Left) were selected as a known age sample. Cosmogenic ¹⁰Be depth-profile ages on detrital sand and pebble from a trench on the same terrace several km to the west from our study area (Fig. 1 CRN sample) are 8.0 ± 1.1 ka and 8.8 ± 1.5 ka, respectively (Thompson, 2013). The OSL samples we collected are deposited on top of the same terrace surface, should be younger than 8.0 ka.

Fig. 2

Location of the modern sample LED11-7 (Left); Trench wall showing the location of samples LED11-1, 11-2 and 11-6 (Right).

The OSL samples were collected in stainless steel tubes (length 15–20 cm, diameter 6 cm). Both ends were immediately sealed with aluminium foil and taped to prevent light leakage and loss of water during transport and storage. The samples were extracted from the inner part of the tubes and quartz was purified using conventional sample preparation techniques (dissolving carbonates with 10% HCl, oxidizing organic matter with 10% H₂O₂, settling using Stokes’ Law, dissolving feldspars by 30% fluorosilicic acid, followed by immersion in 10% HC) for the 4–11 µm fine grain quartz (FQ) fraction (Aitken, 1998; Liu et al., 2010), and 180–250 µm coarse grain quartz (CQ) fractions (sieving, 10% HCl, 10% H₂O₂, etching with 40% HF, followed by immersion in 10% HCl). The purity of the quartz extracts was confirmed by the absence of an IRSL signal for both FQ and CQ. Subsamples of FQ had IR signals close to background levels (Fig. 3a), with an IR-OSL depletion ratio between 0.9 and 1.1. Nevertheless, an IR-OSL depletion test (Duller, 2003) was carried out on every aliquot for small aliquot CQ and single grain (SG) quartz. All the D_e values of samples were measured on a Risø TL/OSL Reader model DA-20 equipped with a calibrated ⁹⁰Sr/⁹⁰Y beta radiation source (dose rate 0.1125 Gy/s for CQ and 0.1045 Gy/s for FQ in the standard configuration), blue (470 ± 30 nm; ~50 mW/cm²) and infrared (880 ± 40 nm, ~145 mW/cm²) light sources, and detection through a 7-mm thick U-340 glass filter.

Fig. 3

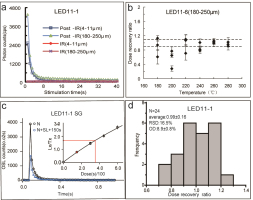
Luminescence characteristics. a – Quartz purity IR check; b – Dose recovery as a function of preheat temperature for coarse grains quartz; c – OSL decay curves for single quartz grains from sample LED11-1, the inset shows a corresponding dose response curve (DRC), the red point is recycling point; d – A histogram of dose recovery ratios for single quartz grains using a 10 s preheat at 260°C for and a 220°C cutheat.

Equivalent dose measurements

Fine grain and single grain quartz

The FQ were measured using a sensitivity-corrected (by a test dose) multiple aliquot regenerative-dose (SMAR) protocol (Lu et al., 2007; Liu et al., 2010). At least six aliquots were measured to determine the natural OSL intensity, and the dose response curve (DRC) was constructed from five aliquots that brackets the natural (normalized) OSL signal (Fig. 4a). In general, the D_e values of the fine grain quartz using SMAR protocol are similar to those of the SAR protocol (Lu et al., 2007; Liu et al., 2010; Yang et al., 2012). We have compared the results of SMAR and SAR protocol of the fine grain quartz for one sample. Both results are the same. But the SMAR protocol can save much more measurement time. So we used the SMAR protocol for fine grain size quartz.

Fig. 4

a – Sensitivity-corrected multiple aliquot regenerative-dose growth curve (SMAR) of sample LED11-1; b – OSL decay curves of sample LED11-1; c – A SAR growth curve; d – Coarse grain quartz small aliquot standardized growth curve (SA-DRC). The red diamonds are sample-specific and were projected on the SA-DRC.

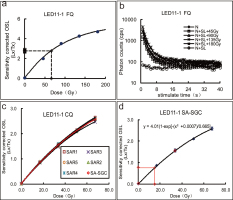
We used the SAR protocol (Murray and Wintle, 2000, 2003; Kortekaas et al., 2007) for the SG quartz measurements. Typical natural and regenerative luminescence signals are shown in Fig. 3c.

Small aliquot coarse grain quartz standardised growth curve (SA-SGC)

Single grain results show that only 1.5–3.7% of the grains yield a detectable OSL signal, a very time consuming endeavour considering that >95% of the grains were without any signal. To improve efficiency, we measured very small aliquots (~80–220 grains per disc as observed under the microscope), as most likely only one or two quartz grains on each disc give a signal, mimicking single grain measurements (Arnold et al., 2012; Medialdea et al., 2014; Faershtein et al., 2016). The SA-SGC was used to measure a large number of D_e values: first a well constrained SAR DRC was constructed for each sample using 5–7 large aliquots from each sample (Fig. 4c), then the L_n/T_n, a zero dose point and one regenerative dose point were measured for a large number (up to 144) of small aliquots (Fig. 4d). The L_n/T_n of each individual small aliquot was projected on the sample-specific DRC to calculate the De for that particular aliquot. Aliquots were rejected if the single regenerative dose point did not lie on the SA-SGC within SA-SGC errors. This procedure is advantageous for samples with heterogeneous resetting of the OSL signal prior to deposition, as it allowed rapid measurements of a large number of small aliquots that could be later used for calculating a meaningful D_e (Table 2).

Table 1

Dose rate results for the samples.

Sample No.	Depth (m)	U (ppm)	Th (ppm)	K (%)	Water contenta (%)	Dose rate (Gy/ka)
						CQ	FQ
LED11-1	2.4	1.65	5.3	1.37	5 ± 5	2.1 ± 0.1	2.9 ± 0.2
LED11-2	2.8	1.74	4.84	1.15	5 ± 5	2.0 ± 0.1	2.6 ± 0.1
LED11-6	0.6	1.96	7.75	1.49	2 ± 2	2.7 ± 0.2	3.4 ± 0.2
LED11-7	0.2	1.35	4.67	1.2	2 ± 2	2.1 ± 0.1	2.5 ± 0.1

a Water contents were estimated at 5 ± 5% or 2 ± 2%

Table 2

D_e values of single grains, small aliquot SA-SGC and fine grains for the samples shown on Fig 2.

Sample No.	Single grains					Small aliquot SA-SGC					Fine grains
	n/Na	Pb (%)	ODc (%)	Ded (Gy)	Age (ka)	n/Na	Pb (%)	ODc (%)	Ded (Gy)	Age (ka)	De (Gy)	Age (ka)
LED11-1	158/4800	3.3	45	14.3−1.7+1.9	6.7−0.9+1.0	43/78	55	36	14.3−3.0+3.3	6.7−1.5+1.6	65.7 ± 5.4	22.9 ± 1.9
LED11-2	55/2300	2.4	62	9.6−1.9+2.5	4.9−1.0+1.3	63/142	44	59	9.8−1.8+3.0	5.0−1.0+1.6	157.6 ± 14.3	60.5 ± 5.4
LED11-6	55/3700	1.5	45	5.2−1.0+1.4	2.0−0.4+0.5	52/144	40	33	5.4−0.5+1.1	2.0−0.2+0.6	66.8 ± 3.1	19.5 ± 0.9
LED11-7	53/1800	2.9	80	0.2−0.1+0.2	0.1−0.05+0.1	42/88	47	59	0.3−0.2+0.3	0.15−0.1+0.15	7.0 ± 0.3	2.8 ± 0.1

a n represents the number of accepted single grains or small aliquots that passed the SAR rejection criteria and used for D_e determination, N represents total number of grains or aliquots measured;

b Proportion (%) of the grains or aliquots that have a detectable OSL signal;

c over-dispersion;

d D_e obtained using the minimum age model.

a n represents the number of accepted single grains or small aliquots that passed the SAR rejection criteria and used for D_e determination, N represents total number of grains or aliquots measured;

b Proportion (%) of the grains or aliquots that have a detectable OSL signal;

c over-dispersion;

d D_e obtained using the minimum age model.

3. Results

As Table 2 shows, the D_e values of FQ range from 7.0 Gy to 158 Gy and the ages from 2.8 ka to 60.5 ka. For SG, we measured a sufficient number of grains so that there were more than fifty accepted for every sample. The percentage of grains with detected signal is lower than 4%. The over-dispersion values range from 45% to 80%. They are higher than average value 20% comparing with the global overdispersion datasets (Arnold and Roberts, 2009). It may be caused different by degrees of the signal resetting. Therefore we used the four parameter version of the minimum age model (Galbraith et al., 1999) which can be used by a likelihood ratio test such as the maximum log likelihood (Lmax higher than 1.92) to isolate the best bleached grains and calculate the most representative D_e values. In the four-parameter version (MAM-4), δ_i is drawn from a population in which a proportion ρ of values are equal to ɤ and the remaining values are larger, having a normal distribution with parameters μ and σ truncated at ɤ. Therefore, exp(ɤ) represents the minimum true dose (in Gy) of the population (Arnold et al., 2009). Prior to running the MAM-4, we added, in quadrature, an overdispersion value of 20% to each individual measured D_e error, to represent the underlying dose overdispersion typically present in well-bleached and undisturbed samples (Arnold and Roberts, 2009; Arnold et al., 2009). The D_e values and ages range from 0.2−0.1+0.2 Gy to 14.3−1.7+1.9 Gy and from 0.1−0.05+0.1 ka to 6.7−0.9+1.0 ka, respectively. For the same samples we measured at least forty accepted small aliquots that passed the SAR rejection criteria for each sample using CQ SA-SGC. The proportion of the accepted aliquots, 40–55%, is much higher than for single grains, and the over-dispersion values range from 33% to 59%, lower than for SG. The D_e values and ages range from 0.3−0.2+0.3 Gy to14.3−3.0+3.3 Gy and from 0.15−0.1+0.15 Ka to 6.7−1.5+1.6 ka, respectively.

4. Discussion

Our study compared OSL ages from different grain-size fractions with different techniques based on the same sample. Ideally a sample should give similar ages for different grain-size fractions and different protocols, but this was not the case. We have one modern sample (LED11-7) deposited after 1985 as an independent age control. We did not find any carbon in the sequence. The depositional environments are fluvial and pluvial deposition in the arid mountainous regions. For FQ, the ages in the trench section are not in chronological sequence and all the ages are much older than the cosmogenic ¹⁰Be ages of 8–8.8 ka. The age of the modern sample LED11-7 is 2.8 ± 0.1 ka, overestimating the true modern age. D_e values of the FQ are 5 to 17 times higher than CQ. The apparent overestimation of OSL ages most likely results from the different aliquot size used for fine and coarse grains. For each of these different measurements, there is a very different number of grains on the disc that contribute to the luminescence signal. Roughly one million grains are present on a fine grain aliquot, an abundance that averages any grain-to-grain dose variations (Wallinga, 2002; Duller, 2008). This averaging masks the poorly bleached grains and results in an overestimation of the true depositional age of the sediment. Therefor fine grain quartz OSL dating is not suitable for such pluvial sediment in association with paleo-earthquakes.

SG ages show a good chronological sequence in the trench section. The MAM age of the modern sample LED11-7 is 0.1−0.05+0.1 ka, sufficiently close to the zero. It shows that this modern analogue is representative of depositional environments, partial bleaching is not the cause using single grains and coarse grain SA-SGC. The lowest sample from the trench located on the terrace (LED11-1) gave a MAM age of 6.7−0.9+1.0 ka, consistent with the cosmogenic ¹⁰Be. Using single grains can separate the best bleached grains from the entire grain population, implying that the single grain results are much closer to the true ages. We suggest that SG measurements combined with the appropriate model is suitable for optical dating of poorly bleached sediments associated with paleo-earthquakes, a conclusion similar to that reached by Porat et al. (2009).

The small aliquots of the SA-SGC have ~80–220 grains per disc; with the small fraction of luminescent grains (1.5–3.7% of the grains emit a luminescence signal according to the single grain results), only 1–2 grains give a luminescence signal on each small aliquot. In addition, the D_e values and ages obtained by the SA-SGC are, within errors, the same as those measured for single grains. In fact, the D_e value calculated for sample LED11-2 using 49 (2-mm) aliquots is 19.5−3.8+6.4 Gy, however when additional smaller aliquots were measured (~50–120 grains, 1 mm disc), a D_e of 9.8−1.8+3.0 Gy was obtained using MAM3, similar to the single grains results. Measuring coarse grain quartz using SA-SGC instead of SG provides a time-saving procedure when dating heterogeneously bleached sediments, with results similar to that of SG. But it is necessary to ensure that there is a small enough number of grains on a disc and enough accepted aliquots.

5. Conclusions

In this study, fine grains quartz measurements overestimated the expected D_e values and were much older than single grains and coarse grain SA-SGC. The residual dose 0.2−0.1+0.2 Gy measured using single grains of the modern sample is insignificant when dating samples which are thousands of years old in paleo-earthquake settings. Only 1.5–3.6% of the coarse-grain quartz have a detectable OSL signal. The ages measured for three samples in the trench section using single grains are in stratigraphic sequence and are consistent with that of the cosmogenic ¹⁰Be dating, indicating that such samples might be suitable for optical dating of paleo-earthquakes. Coarse grains SA-SGC D_e values are similar to those measured for single grains. This is an efficient way to measure poorly bleached quartz which has good potential for future studies of paleo-earthquakes. Notably, enough accepted grains or aliquots are required for calculating D_e values. Detailed and thorough scientific studies should be carried out in order to improve accuracy for paleo-earthquake ages. We recommend using caution when interpreting ages derived from fine grain measurements.

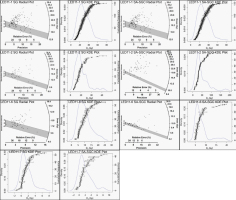
Fig. 5

Radial plots and KDE plots from single grains (SG) and small aliquot standardised growth curve (SA-SGC) for samples LED11-1, LED11-2 and LED11-6. Grey bands on radial plots show the samples’ De values with 2-sigma error (Table 2). Only KDE plots are shown for the sample LED11-7.