. Introduction
The growth of trees is controlled by genetic factors and natural environment. Multiple climatic factors of the growth environment directly influence the development of tree rings (Esper et al., 2002; Büntgen et al., 2011). The northernmost and largest coniferous forest in China distributes over the whole Greater Higgnan Mountains, at the fringe of the East Asian monsoon. This region has experienced a strong temperature increase since the 1980s (Sun et al., 2005; Tang and Ren, 2005). Understanding the relationships between climate factors and the radial growth of coniferous trees within this sensitive region of climatic change could provide insights into the long-term dynamics of primitive forest under the background of global warming.
Tree-ring samples in the Greater Higgnan Mountains have been systematically collected since the year 2000 (He et al., 2005). Many dendroclimatogical studies related to tree-ring width (Zhang et al., 2009) and tree-ring density (Wang et al., 2005) data from two main local tree species, Larix gmelinii and Pinus sylvestris var. mongolica, have been carried out in the Greater Higgnan Mountains. Sun et al. (2010) showed that the ring-width chronology of larch trees from the Mohe region in the northern Greater Higgnan Mountains correlate positively with temperature in August (p < 0.05), whereas radial growth of the same species in the middle of Greater Higgnan Mountains are significantly negatively correlated (p < 0.01) with temperatures in May and July (Zhang et al., 2010). Centennial-scale reconstructions have been developed based on tree-ring data from the central and northern Greater Higgnan Mountains (Liu et al., 2009a; Bao et al., 2012; Sun et al., 2012b; Zhang et al., 2013; Zhang et al., 2014a). In contrast, dendroclimatogical studies from the southern Greater Higgnan Mountains are relatively limited.
Given the above, the purposes of this study are to (1) develop tree-ring chronologies for the southern Greater Higgnan Mountains, (2) explore the climate controls of radial growth of larch trees, (3) and statistically assess signals inherent in a newly developed regional tree-ring chronology.
. Materials and methods
Sample collection
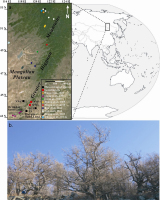
The Greater Higgnan Mountains, extending more than 1200 km in lengthways direction and 200–300 km in sideways direction, are on the northeastern Asian continent. These huge mountain ranges merge with the Stanovoy Mountains in the north and their southern extent meets the eastern Ortindag Sand Land. Our sampling targeted the southern Greater Higgnan Mountains (Fig. 1a). The tree species studied was the larch (Larix principis-rupprechtii), which usually grow higher than 30 m. Forest stands of the study area are relatively open and canopy densities of the larch are low (Fig. 1b). Haplic Chernozems were the soil type under the sampled trees (FAO et al., 2012). Information regarding sampling sites is provided in Table 1, such as location, environment, and tree age. We tended to select healthy larch trees with little evidence of bushfire, landslide, or human/animal disturbance to avoid sampling of non-climatic effects on radial growth. For most sampled trees, we extracted two cores from different directions. A total of 82 cores from 41 trees were collected from sites Baiyinhanshan (BYH) and Qianmugou (QMG) with increment borers (5.15-mm diameter). The oldest tree at BYH was nearly 224 years in age.
Fig. 1
Location of tree-ring sites sampled in this study and selected from previous studies (Wang et al., 2005; Liang et al., 2007a; Liu et al., 2009a; Zhang et al., 2009; Zhang et al., 2010; Bao et al., 2012; Sun et al., 2012b; Zhang et al., 2013; Zhang et al., 2014a) and meteorological stations in Greater Higgnan Mountains (a); a display of sampling environment in the study area (b).
Chronology development
According to standard dendrochronological techniques (Speer, 2010), the sampled tree-ring cores were dried naturally and mounted on a wooden plank with grooves. Then, each tree-ring core was sanded with abrasive papers and marked with needles under a microscope. Every ring on the sanded tree-ring cores was measured by a Velmex Measuring System at resolution 0.001 mm. The COFECHA and ARSTAN programs were run to control cross-dating quality and develop chronologies (Grissino-Mayer, 2001; Cook and Krusic, 2005). A negative exponential function was executed for tree-ring width series detrending. Then, all individual detrended ring-width series were combined into a single chronology by computing a bi-weight robust mean. Eventually, standardized, residual and autoregressive standardized tree-ring chronologies were obtained (Cook and Kairiukstis, 1990). The reliability of the tree-ring chronology was evaluated by an expressed population signal (EPS) (Wigley et al., 1984). The statistical analyses were done in 20-year intervals with an overlap of 10 years across the chronology. An EPS of ≥ 0.85 was used to ensure a reliable chronology length (Esper et al., 2003). Thus, reliable lengths of the BYH and QMG chronologies were respectively 185 (1830–2014) and 65 (1950–2014) years.
Climatic data
For calibration, we selected monthly precipitation and mean temperature at the Balinzuoqi (119°24′E, 43°59′N, 485.9 m a.s.l., 1955–2012), Xiwuzhumuqinqi (117°36′E, 44°35′N, 996.6 m a.s.l., 1955–2012) and Linxi (118°04′E, 43°36′N, 800.3 m a.s.l., 1955–2012) meteorological stations, and monthly 118.25°E–44.25°N Palmer Drought Severity Index (PDSI), which is derived from a Climatic Research Unit (CRU) self-calibrating PDSI dataset (Mitchell and Jones, 2005). The above climatic data were acquired from the China Monthly Surface Climatological Database (NMIC, 2008) and Royal Netherlands Meteorological Institute Climate Explorer, respectively.
Fig. 2 shows that the highest temperature periods were in summer (June–August) in the study area, with peaks in July. June–August precipitation comprises the major portion of annual rainfall, with maximum precipitation in July. Climate data recorded since 1955 show a significant increasing trend of annual mean temperature in the study area, but a decreasing trend of annual precipitation is not significant. Fig. 3a reveals that the driest period peaks in August (PDSI of –0.63), and the wettest month is in April (–0.28). And Fig. 3b shows that the decreasing trend of annual PDSI is not significant. Furthermore, correlation coefficients of the annual precipitation and mean temperature from the three meteorological stations are all significant in the original and first differences domain (Table 2). Owing to their similar monthly and annual variations, simple averaging was done on the instrumental data from those meteorological stations to obtain overall climatic conditions in the study area.
Fig. 2
Climatic diagram for Balinzuoqi (a, b, c), Xiwuzhumuqinqi (d, e, f) and Linxi (g, h, i) meteorological stations near sampling sites in southern Greater Higgnan Mountains, and average meteorological data from the three stations (j, k, l). Bars indicate monthly precipitation (mm), and curves with points represent monthly mean temperature (°C). Solid lines indicate annual total precipitation and mean temperature. Dashed lines represent trends of annual climatic data.
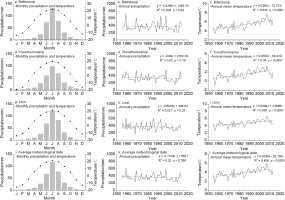
Fig. 3
Monthly (a) and annual (b) mean PDSI for southern Greater Higgnan Mountains. Dashed lines represent trends of annual mean PDSI.
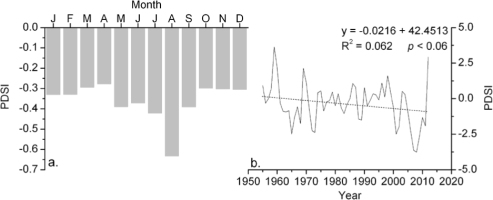
Table 2
Coherence among annual total precipitation and annual mean temperature from three meteorological stations over the common period 1955–2012. Correlation coefficients are listed. Results for the original and first differences filtered climatic data are shown.
| Original (n = 59)/The first differences (n = 58) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Annual total precipitation | Annual mean temperature | |||||||
| Balinzuoqi | Xiwuzhumuqinqi | Linxi | Balinzuoqi | Xiwuzhumuqinqi | Linxi | |||
| Balinzuoqi | / | 0.599*/0.520* | 0.638*/0.610* | / | / | / | ||
| Annual total precipitation | Xiwuzhumuqinqi | / | / | 0.646*/0.637* | / | / | / | |
| Linxi | / | / | / | / | / | / | ||
| Balinzuoqi | / | / | / | / | 0.904*/0.900* | 0.947*/0.947* | ||
| Annual mean temperature | Xiwuzhumuqinqi | / | / | / | / | / | 0.950*/0.935* | |
| Linxi | / | / | / | / | / | / | ||
Statistical analysis
A 13-year reciprocal filter was used to decompose the newly developed tree-ring width chronologies into high- and low-frequency domains (Yuan et al., 2013). Variation patterns of these original and decomposed chronologies were assessed by Pearson correlation. Correlation analyses were also used to evaluate the strengths of tree growth climate response and climatic signals inherent in tree-ring width chronologies from larch trees in the study area. Spatial correlation was used to identify coherence between the chronologies and the gridded climatic data in a large region. The gridded 0.5° × 0.5° CRU time-series 3.23 (land) dataset and 0.5° CRU self-calibrating PDSI 3.21 dataset were used in the spatial correlation (Mitchell and Jones, 2005).
. Results and discussion
Chronology development and statistical analyses
A standardized chronology not only contains common variations among each tree-ring series but also retains high- and low-frequency common variance (Cook, 1985). Thus, the standardized chronologies of two sampling sites were used in the following analyses. Because of the weak correlations between subsequences from each tree-ring width series and the master series, 10 cores from 9 trees at the BYH and QMG sites were not used to develop chronologies. Thus, the BYH and QMG chronologies were developed based on 38 cores from 20 trees and 34 tree-ring cores from 20 larch trees, respectively. The BYH and QMG chronologies are displayed with their EPS values in Fig. 4. Statistics of these chronologies for a common period analysis of 1950 to 2010 are listed in Table 3.
Fig. 4
Two tree-ring-width chronologies (thin lines) from single sample site, and regional chronology and EPS data (thick lines). Dashed lines represent EPS = 0.85.
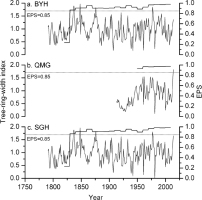
Table 3
Statistics of chronologies from two sampling sites (BYH and QMG) and regional chronology (SGH) over common period 1950–2010.
Both tree-ring width chronologies were decomposed into high- and low-pass components using 13-year reciprocal filters. Next, Pearson correlation was performed on three sets of data, i.e., original unfiltered, high-pass filtered, and low-pass filtered. Table 4 reveals that although correlation between two chronologies using the low-pass filter is relatively weak, correlation coefficients in the original, high-, and low-frequency domains all surpass the 99.9% confidence level. Because of strong correlations between chronologies of a single sampling site, all tree-ring width series were combined to construct a chronology SGH) to represent regional radial growth. The SGH chronology was developed following the method mentioned in the preceding text. Fig. 4c presents the SGH chronology and its reliable length based on EPS values.
Table 4
Coherence among chronologies from two sampling sites over common period 1950–2014. Correlation coefficients are listed. Results for the original, high- and low-pass filtered chronologies are shown.
| Original | High-frequency | Low-frequency | |
|---|---|---|---|
| r | 0.572 | 0.681 | 0.501 |
| p | < 0.001 | < 0.001 | < 0.001 |
| n | 65 | 53 | 53 |
The main descriptive statistics of this regional chronology are listed in Table 3. Values of standard deviation (0.35) and mean sensitivity (0.32), indicators of climatic signals inherent in the regional chronology, are similar to those of chronologies from a single sample site. The first-order autocorrelation estimates relationships between present tree rings and growth in a previous year. These values (from 0.44 to 0.60) indicate that the chronologies contain low-frequency variance caused by climate and tree-physiological lag effects. These interseries correlations of the SGH chronology are relatively weak, owing to an increase of sample depth from two individual sites. EPS values exceeding 0.85 reveal that the credible regional chronology spans 185 years (1830–2014). Ten highest values of the SGH chronology are in 1848 (1.957), 1837 (1.881), 1876 (1.829), 1977 (1.807), 1836 (1.767), 1838 (1.655), 2014 (1.654), 1921 (1.617), 1874 (1.606) and 1978 (1.598), and ten lowest values are in 1981 (0.019), 1942 (0.087), 1961 (0.136), 1939 (0.193), 1907 (0.219), 1886 (0.392), 2000 (0.441), 1883 (0.455), 1924 (0.466) and 1922 (0.479).
Tree growth climate response
The high AC1 values of two individual and one composite chronologies (0.46, 0.60, and 0.44, respectively) indicates a significant biological lag effect in the process of tree growth (Table 3). Thus, average meteorological data of the previous August–December and current January–October during 1955–2012 were selected to evaluate how variations of precipitation and temperature influenced the radial growth of larch trees in the southern Greater Higgnan Mountains.
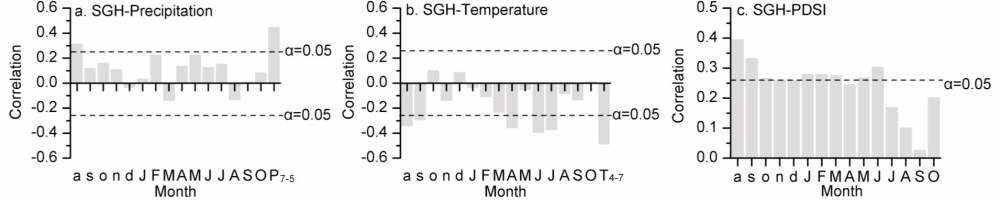
The results of correlation (Fig. 5) indicate that the relationship between ring width and precipitation was generally positive, and a significant correlation coefficient was found for August of the previous year (r = 0.312, p < 0.02, n = 57). The response of radial growth of larch trees to temperature was negative, and the SGH chronology was negatively correlated with mean temperature of the previous August (r = –0.340, n = 57) and September (r = –0.293, n = 57), and current April (r = –0.355, n = 58), June (r = –0.393, n = 58) and July (r = –0.372, n = 58), at the 95% confidence level. After testing various combinations of months, we found a larger correlation coefficient between the SGH chronology and precipitation for the period between the previous July and current May (r = 0.445, p < 0.001, n = 57). The regional chronology and April–July mean temperature had the strongest relationship (r = –0.486, p < 0.001, n = 58). The monthly 118.25°E–44.25°N PDSI from the previous August to current October during 1955–2012 was also used to correlate with the regional chronology. Significant correlations were found from the previous August to current June (except April) based on the 95% confidence level, peaking in the previous August. The above results reveal that correlation coefficients between tree-ring width and climatic data are relatively small. A previous study indicated that Larix principis-rupprechtii always grow in an altitudinal gradient from 1200 to 2800 m a.s.l. (Liang et al., 2007b). Because of the limits of landforms in the study area, we collected tree-ring samples from 1300 to 1500 m a.s.l. (Table 1). The altitude of sampling sites may affect the results of tree growth climate response.
Fig. 5
Pearson correlations (bars) among SGH chronology and average meteorological data from three stations (a. precipitation; b. mean temperature), and (c) gridded 118.25°–44.25° PDSI. Lowercase letters represent months of previous year, and uppercase letters are months of current year. P7-5 indicates precipitation from previous July to current May; T4–7 indicates temperature from April to July. Dotted lines indicate 0.05 significance levels.
The photosynthetic optimum temperature for evergreen conifer ranges from 10°C to 25°C. Photosynthesis in these conifer trees may cease at temperatures below –3°C to –5°C or above 35°C to 42°C (Wang, 2000). Fig. 2j reveals that the mean temperature from April to October changed from 6.0°C to 4.9°C, and those in March and November were –4.5°C and –5.5°C, respectively. Therefore, April–October has been regarded as the growth season of larch trees in the study area. Furthermore, Li et al. (2013) studied evapotranspiration during the growing season of Larix principis-rupprechtii in the Liupan Mountains of northwestern China. The results show that these larch trees usually sprout in mid-April. The stand canopy of these trees becomes largest from late July to early August, decreasing quickly in September and October.
Studies of conifers and the relationship between treering width and climate in arid and semiarid locations have gradually demonstrated that ring-width growth is not only influenced by climate during the growing season but also that in autumn, winter, and spring prior to the growing season (Kitin et al., 1999). The period from the previous July to current May can be divided into three parts. The first part (July–October in the previous year) is the middle to late growth season of larch trees in the Greater Higgnan Mountains. Greater precipitation in this period leads to enhanced accumulation of photosynthetic products, resulting in an abundance of larger leaves, buds, and roots. This increases the total photosynthetic and absorptive areas of the trees, such that they are able to photosynthesize or absorb moisture when there are favorable climatic conditions occur in the following year (Liu et al., 2011). The second part (from the previous November to current March) is the non-growth season of larch trees. Snowfall comprises a major proportion of total precipitation during this period. Greater snowfall in the non-growth season means that trees may absorb more moisture in the subsequent growing season (D’Arrigo and Jacoby, 1991; Díaz et al., 2002). The third part (April–May of the current year) is the beginning of larch tree growth. In this period, additional rainfall producing greater soil moisture may reduce water stress and benefit cambial cell division in the rapid growth season (Liu et al., 2004).
Temperature always affects the radial growth of trees by modulating the amount of soil moisture in arid and semiarid areas (Zhang et al., 2014b). For this reason, correlation between tree-ring width and temperature was negative in the growth season. April–July spans the beginning of the tree growth season to the rapid growth season. High temperature in this period may directly limit tree growth by enhancing evapotranspiration in arid and semiarid areas (Bao et al., 2012).
The significant positive correlations between the radial growth of trees and PDSI demonstrate the primary combined influence of precipitation and mean temperature. Greater moisture from the previous August to current June may reduce water stress and benefit cambial cell division in the rapid growth season. Thus, the positive relationship with rainfall, negative response to temperature, and positive correlations with PDSI indicate that moisture was the main climatic limitation on tree-ring development of larch trees in the study area. The above results show that the influence of moisture on tree-ring growth in the southern Greater Higgnan Mountains is the same as indicated by dendroclimatic studies of northern China, such as Pinus sylvestris var. mongolica on the eastern Mongolian Plateau (Bao et al., 2015), Pinus tabulaeformis Carr. in the Ortindag Sand Land (Liang et al., 2007a) and central Taihang Mountains (Cai and Liu, 2013), Pinus tabulaeformis in the Fenhe River basin (Sun et al., 2012a) and in the Kongtong Mountains (Song and Liu, 2011), and Sabina przewalskii in the northwestern Qilian Mountains (Liu et al., 2009b).
Comparison with PDSI
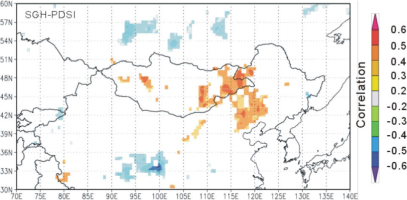
The spatial correlation was determined to evaluate regional significance of the tree-ring width series. The PDSI periods were used in the spatial correlation based on the results of correlation analysis mentioned above. The results show that the SGH chronology is correlated (< 0.3) with the August–June gridded PDSI data for the eastern Mongolian Plateau and Nuluerhu Mountains during the period 1955–2012 (Fig. 6). This suggests that the radial growth of trees in the study area not only reflect local climate change but also contain large-scale climatic signals.
Fig. 6
Spatial correlation of the regional chronology for southern Greater Higgnan Mountains from 0.5° CRU self-calibrating PDSI 3.21 dataset over the period 1955–2012.
A May–July PDSI reconstruction for the Ortindag Sand Land based on tree-ring width (Liang et al., 2007a) was compared with the newly developed regional chronology. The lowest values (< –4.0) of the PDSI reconstruction were in 1865, 1968, 1981, 1989 and 2001. Two lowest values in the SGH chronology in 1981 and 2000 coincide with the lowest PDSI values in those years for Ortindag Sand Land. A previous study revealed a severe and sustained drought in the 1920s across a wide area of northern China, based on a network of tree-ring data (Liang et al., 2006). Associated with this drought, there are two minimum values (in 1922 and 1924) within the SGH chronology.
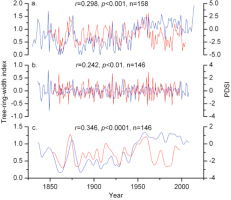
The SGH chronology is positively correlated with the PDSI reconstruction over the common period 1847–2004, at the 99.9% confidence level (r = 0.298, n = 158). The SGH chronology and PDSI reconstruction were also decomposed by 13-year reciprocal filters to assess their coherence (Fig. 7). Correlation coefficients between the tree-ring width chronology and PDSI reconstruction were 0.242 in the high-frequency domain and 0.346 in the low-frequency domain. The horizontal distance between our sampling sites and those in Ortindag Sand Land is nearly 130 km. We believe that there are three reasons for the relatively weak relationship between the PDSI reconstruction in Liang et al. (2007a) and regional chronology SGH. First, the species of the sampled trees are Pinus tabulaeformis Carr. and Larix principis-rupprechtii. Physiological characteristics of the two kinds of needleleaved trees may be different. Second, the underlying surface conditions are different. In our study area, the sampled trees were growing on Haplic Chernozems in a mountainous area, whereas the trees studied by Liang et al. (2007a) were on sand in a desert area. These contrasting underlying surfaces lead to a difference in principal climatic limitation. The May–July PDSI limited tree growth in Ortindag Sand Land, whereas annual moisture variations altered radial growth of the sampled trees in the southern Greater Higgnan Mountains. Finally, the correlation coefficient between May–July and August–June PDSI of the study area is r = 0.779 (p < 0.001, n = 57). Although the correlation is not strong, long-term trends of the chronology and reconstruction are very similar in the low-frequency domain (Fig. 7c). Decadal variability was highlighted by applying the 13-year reciprocal filters to the SGH chronology, from which three large-value and two small-value periods could be distinguished. The former periods were 1836–1852, 1872–1878 and 1944–2008, and the latter value periods were 1853–1871 and 1879–1943. Two small-value periods (1853–1871 and 1879–1943) coincide with the dry periods 1853–1883 in the Chifeng-Weichang region (Liu et al., 2010) and 1888–1929 in the Hailar region (Liu et al., 2009a), which are attributable to a weak monsoon.
. Conclusions
A 185-year regional tree-ring width chronology was developed using 41 living larch trees selected from two sampling sites in the southern Greater Higgnan Mountains. The relationship between precipitation and tree growth was generally positive, but correlations between monthly mean temperature and the regional chronology are mostly negative. The results of tree growth climate response revealed that moisture was the main climatic limitation on the radial growth of larch trees at the sampling sites. The analyses of spatial correlation reveal positive correlations between the regional chronology and gridded PDSI dataset for the Nuluerhu Mountains and eastern Mongolian Plateau. The comparison between the regional chronology and May–July PDSI reconstruction for Ortindag Sand Land indicates that the radial growth of larch trees in the southern Greater Higgnan Mountains and moisture variations in adjacent areas were roughly synchronous over the last nearly 160 years, especially in the low-frequency domain. Furthermore, two lowest values in the newly developed chronology coincided with a severe and sustained drought in the 1920s across a wide area of northern China.