1. Introduction

Dating of hydrothermal deposits is an important issue in the studies of the evolution of the sea floor hydrothermal fields where geochronological dating methods applied to hydrothermal deposits are the key techniques. Dating methods using radioactive disequilibrium have been employed for hydrothermal sulfide deposits, such as the U-Th method (e.g. You and Bickle,1998) for sulfide minerals applicable for the age range more than several thousand years, and ²²⁶Ra-²¹⁰Pb and ²²⁸Ra-²²⁸Th methods (e.g. Noguchi et al., 2011) for barite extracted from sulfide deposits for the range less than 150 years. Although the age range of several hundred years is essential to estimate the life time of hydrothermal activities, dating methods for this age range were lacking.

Kasuya et al. (1991) investigated the dose responses of the electron spin resonance (ESR) signals observed in natural barite samples and first pointed out that ESR dating of barite is possible. Following Okumura et al. (2010), who made the first practical application of ESR dating to a sample of seafloor hydrothermal barite with the signal due to so3−, basic studies on ESR dating of barite were performed by Toyoda et al. (2011) for the optimum conditions of ESR measurements of the dating signal, by Sato et al. (2011) for the thermal stability of the signal, and by Toyoda et al. (2012) for the alpha effectiveness value.

Takamasa et al. (2013) examined sulfide deposits in the South Mariana Trough sea-floor hydrothermal field to compare the ESR ages obtained for barite and the U-Th ages for sulfide minerals extracted from the same portions. They showed that the ESR ages are roughly consistent with the U-Th ages. While Toyoda et al. (2014) discussed several detailed technical issues such as the dose rate conversion factors, the sample edge effect for gamma ray dose, and the correction for the decay of ²²⁶Ra, Fujiwara et al. (2015) made the first practical systematic dating work with ESR on barite of sea-floor hydrothermal sulfide deposits taken at Okinawa Trough on total of 18 samples (60 subsamples) with new formulas which take the radioactive disequilibrium of Ra daughter nuclei into account. The obtained ages range 4 to 16000 years, showing that the ESR method has a wide application age range. Uchida et al. (2015) obtained ²²⁶Ra-²¹⁰Pb and ²²⁸Ra-²²⁸Th ages for the same samples as Fujiwara et al. (2015) analyzed and attributed the differences of the ages among these three dating methods to possible multiple formation stages of the sulfide deposits.

2. Issues in determining dose rates to barite extracted from sea-floor hydrothermal sulfide deposits

When hydrothermal fluid containing barium ions is mixed with sea water, they react with sulfate ions in the sea water to precipitate barite (barium sulfate, BaSO₄). The barite crystals occur in sulfide chimneys and in deposits, incorporating radium ions that are in the hydrothermal fluid. As a radium ion has an ionic radius similar with barium, radium ions easily replace barium in barite to have high concentration up to several tens Bq/g of ²²⁶Ra (Fujiwara et al., 2015).

The source of natural radiation in sulfide deposits containing barite is radium and its daughter nuclei in barite where the doses from the other minerals are negligible (Toyoda et al., 2014). Under these circumstances, the specific issues for the dose rates in calculating the ESR ages are, as summarized by Toyoda et al. (2014), the conversion factors, the calculation of internal and external dose rates including the determination of the alpha effectiveness, the water content, the geometric factors such as the grain sizes, and the radioactive disequilibrium. The radioactive disequilibrium is one of the most complex and important issue in calculating the ESR ages.

While Toyoda et al. (2014) devised a formula to correct the age due to the decay of ²²⁶Ra assuming radioactive equilibrium, Fujiwara et al. (2015) proposed formulas to consider the radioactive disequilibria. The same equation applies both to ²²⁶Ra and ²²⁸Ra series, and the total accumulated natural equivalent dose, D_E(T), which is the summation of the two, is expressed by,

where λ₁, λ₂, λ₃, and λ₄ are the decay constants of ²²⁶Ra, ²¹⁰Pb, ²²⁸Ra, and ²²⁸Th, respectively, Q₁, Q₂, Q₃, and Q₄ are the conversion factors of ²²⁶Ra to ²¹⁴Po, ²¹⁰Pb to ²⁰⁶Pb, ²²⁸Ra and ²²⁸Ac, and ²²⁸Th to ²⁰⁸Pb, respectively, referring to Guérin et al. (2011). λ₁N_lp and λ₃N_3p are the present activity of ²²⁶Ra and ²²⁸Ra, respectively, and T is the age. When the experimentally obtained equivalent dose is D_exp, the equation is,

In order to solve this equation, a function, f(T) is defined as,

and the equation to be solved is deduced to

This non-linear equation can be numerically solved by the Newton method, which is

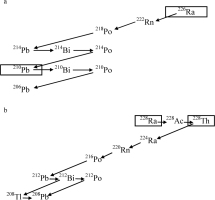
It should be noted that ²¹⁰Pb has the longest half-life of 22.3 y in the decay series after ²²⁶Ra with a half-life of 1600 y (Fig. 1a), and that ²²⁸Th has the longest half-life of 1.91 y in the decay series after ²²⁸Ra with a half-life of 5.75 y (Fig. 1b), therefore, other radioactive disequilibrium can be neglected.

For the samples, in which ²²⁸Ra is observed, the contributions to the natural accumulated dose from the ²²⁸Ra series as well as that from ²²⁶Ra series can be calculated by Eq. 2.1 where the age, T, is obtained as the solution of, Eq. 2.4, as these procedures are actually adopted in obtaining the ESR ages of hydrothermal barite in Okinawa Trough (Fujiwara et al., 2015). As time passes, ²²⁸Ra with a half-life of 5.75 y will decay out so that ²²⁸Ra and its daughter nuclei will not contribute doses any more. Therefore, if the sample is old enough, the contribution of ²²⁸Ra and its daughter nuclei to the natural accumulated dose of barite would be negligible. However, the fact that ²²⁸Ra and its daughter nuclei are not observed would not necessarily guarantee that their contribution is negligible. In the present paper, the evolution of the contribution of each nucleus to the accumulated barite dose is simulated by numerical calculation to find that there is an age range in which the contribution from non-observable ²²⁸Ra and its daughter nuclei cannot be neglected.

Fig. 1

Radioactive decay chains from (a) ²²⁶Ra and (b) ²²⁸Ra.

3. The analysis for the test sample

The simulation of the contribution from ²²⁸Ra and its daughter nuclei to the accumulated dose is made for an actual test sample, HPD1621R03, taken at a sea-floor hydrothermal area at depth of 1495 m of Hatoma Knoll, Okinawa Trough by the research cruise, KY14-02, operated by Japan Agency for Marine-Earth Science and Technology (JAMSTEC). The sample is a portion of sulfide deposit including barite crystals.

The analysis was made according to the procedures described in Fujiwara et al. (2015) and in Uchida et al. (2015). A piece of a block cut out of the deposit was soaked in water for 3 days and its mass was measured. After drying in an oven at 60°C for several days until the weight did not change, the water mass was estimated from the difference in the masses as the ratio of the mass of water to the dry mass to be 30.3%. The sample was then crushed and the bulk concentrations of ²²⁶Ra and ²²⁸Ra were obtained by low background gamma ray spectrometry with a pure Ge detector from the gamma ray peaks due to ²¹⁴Bi and ²¹⁴Pb, and ²²⁸Ac to be 16.9 Bq/g and 1.02 Bq/g, respectively.

The barite crystals were extracted from the crushed bulk sample by using HNO₃ and HF. An XRF measurement was made to confirm that the extracted crystals are pure barite. The mass of barite crystals is 70.0% of the total dry mass before the chemical treatment. The barite grains were separated into 10 aliquots for gamma ray irradiation for the additive dose method. An ESR signal due to so3−, was observed in the samples. From the response of the intensity of the signal to the gamma ray dose, the equivalent dose was obtained to be 20.8−1.5+1.6 Gy by extrapolating the dose response fitted to a saturating exponential curve to the zero ordinate. Using the Eqs. 2.1 to 2.4 with the corrections for the water content and for the grain size which is typically 20 µm in thickness (Fujiwara et al., 2015), with the alpha effectiveness value of 0.043 (Toyoda et al., 2012), and with the consideration for the external and internal β doses, the ESR age for this present sample was estimated to be 33 ± 1 ka as shown in Table 1.

4. Simulation for the contribution of the dose from ²²⁸Ra and daughter nuclei

The contribution of the radiation doses from ²²⁸Ra and its daughter nuclei to the accumulated dose to barite in this test sample, HPD1621R03, is simulated as a function of time as in the following. Based on the ESR age obtained as above, the initial (when the age of the sample is zero) bulk concentrations of ²²⁶Ra and ²²⁸Ra are calculated to be 17.0 Bq/g and 59.4 Bq/g, respectively.

The accumulation of the doses to barite given by the nuclei, ²²⁶Ra to ²¹⁴Po, ²¹⁰Pb to ²⁰⁶Pb, ²²⁸Ra and ²²⁸Ac, and ²²⁸Th to ²⁰⁸Pb are respectively calculated from the following formulas, which are deduced from Eq. 2.1,

where D_E1, D_E2, D_E3, and D_E4 are the doses from ²²⁶Ra to ²¹⁴Po, ²¹⁰Pb to ²⁰⁶Pb, ²²⁸Ra and ²²⁸Ac, and ²²⁸Th to ²⁰⁸Pb, respectively, and N₁₀ and N₃₀ are the initial concentrations of ²²⁶Ra and ²²⁸Ra, respectively.

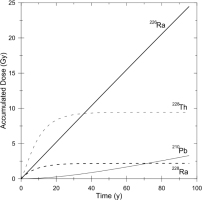
The values of D_E1, D_E2, D_E3, and D_E4 are calculated as a function of time for barite crystals in the sample as shown in Fig. 2. The accumulated dose from ²²⁶Ra to ²¹⁴Po (indicated by ²²⁶Ra in the figure) linearly increases with time as the half-life of ²²⁶Ra, 1600 y, is much larger than the time scale shown in the figure. The one from ²¹⁰Pb to ²⁰⁶Pb (indicated by ²¹⁰Pb) slowly increase and then turns linear increase after equilibrated with ²²⁶Ra. The one from ²²⁸Ra and ²²⁸Ac (indicated by ²²⁸Ra) saturates rapidly meaning that those nuclei decay out rapidly where the half-life of ²²⁸Ra is 5.75 y. It is noted that the dose from ²²⁸Th to ²⁰⁸Pb (indicated by ²²⁸Th) gives a significant contribution when the sample is young. When their parent, ²²⁸Ra, decays out, these nuclei also decay out to give no contribution anymore.

Fig. 2

The results of simulation as a function of time of the accumulated doses given by radioactive nuclei ²²⁶Ra to ²¹⁴Po (indicated by ²²⁶Ra), ²¹⁰Pb to ²⁰⁶Pb (indicated by ²¹⁰Pb), ²²⁸Ra and ²²⁸Ac (indicated by ²²⁸Ra), and ²²⁸Th to ²⁰⁸Pb (indicated by ²²⁸Th). The values are calculated for HPD1621R03, taken at a sea-floor hydrothermal area at depth of 1495 m of Hatoma Knoll, Okinawa Trough, the ESR age of which was estimated to be 33 years while the bulk concentrations of ²²⁶Ra and ²²⁸Ra are estimated to be 17.0 Bq/g and 59.4 Bq/g, respectively.

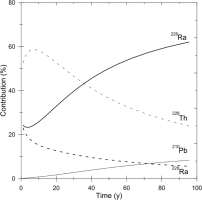
From the values shown in (Fig. 2), the contributions of the accumulated doses are calculated as a function of time and shown in % (Fig. 3) from ²²⁶Ra to ²¹⁴Po, ²¹⁰Pb to ²⁰⁶Pb, ²²⁸Ra and ²²⁸Ac, and ²²⁸Th to ²⁰⁸Pb, indicated by ²⁶Ra, ²¹⁰Pb, ²²⁸Ra, and ²²⁸Th, respectively. The contribution from ²²⁸Th to ²⁰⁸Pb reaches 60% at its maximum and remains still 30% at 100 years when the nuclei have already decayed out.

Fig. 3

The contributions to the accumulated dose as a function of time of the nuclei, ²²⁶Ra to ²¹⁴Po (indicated by ²²⁶Ra), ²¹⁰Pb to ²⁰⁶Pb (indicated by ²¹⁰Pb), ²²⁸Ra and ²²⁸Ac (indicated by ²²⁸Ra), and ²²⁸Th to ²⁰⁸Pb (indicated by ²²⁸Th) in %, calculated from the values in Fig. 1.

For a longer time scale, the contribution to the accumulated dose from ²²⁸Ra series (²²⁸Ra to ²⁰⁸Pb) is calculated as shown in Fig. 4, which is in logarithmic time scale. As shown in the figure, even after 300 years, the contribution from ²²⁸Ra series is sti11 10%. It is obvious that the ESR ages calculated without contribution of ²²⁸Ra series to the accumulated dose will be overestimates. For the present test sample, a simulation indicates that the age will be estimated to be 90 years at age of 50 years when the contribution is not taken into account, while it will still be 360 years, 20% overestimates, at age of 300 year, where the overestimate is comparable as the typical variation, 20%, of the ESR ages from a same portion (Fujiwara et al., 2015) including the measurement error. The overestimate becomes 5% at age of 500 years.

Fig. 4

The contribution to the accumulated dose from ²²⁸Ra series as a function of time in logarithmic scale.

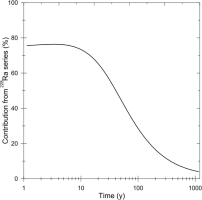
As the half-life of ²²⁸Ra is 5.75 year, although depending on the sample, the nucleus can be detected for young samples. For such young samples, the contribution of the dose from ²²⁸Ra series can be taken into account and the ESR age can be appropriately estimated. For the current test sample, the ²²⁸Ra concentration will become 7×10⁻⁵ Bq/g comparable as the detection limit after 50 years. After this age, the contribution cannot be estimated, because ²²⁸Ra series nuclei have decayed out, but still necessary to be considered according to the above discussion. In summary, the ages of the samples for which the ESR ages have been estimated to be less than 300 years without considering the doses from ²²⁸Ra series, would have probably been overestimated and this would most typically happen for the samples older than 50 years because ²²⁸Ra cannot be detected.Currently, any date over 50 years should be considered a maximum value when the ²²⁸Ra content is not obtained.

How to correct this contribution would be an important but difficult issue. The initial ²²⁸Ra concentration needs to be estimated. For this particular sample examined in the present study, the initial ²²⁸Ra/²²⁶Ra activity ratio is estimated to be 3.49 from the present ²²⁶Ra and ²²⁸Ra concentrations and the ESR age, which is equivalent to virtually equilibrated Th/U ratio (in ppm) of 10.7. This ratio would be a little high but in the reasonable range as material in the crust. One way would be to investigate and accumulate data on the initial ²²⁸Ra/²²⁶Ra activity ratio in young or preferably zero age barite samples or in the hydrothermal fluid.

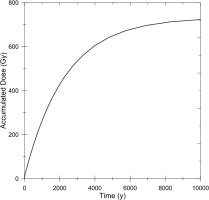
The upper age limit of ESR dating has not been discussed except for the thermal stability, which was estimated to be at least several thousand years (Sato et al., 2011), while the oldest age was reported to be 16000 years (Fujiwara et al., 2015). According to the present simulation of the accumulated dose for further longer time scale, it is found that the dose will be close to saturation after about 5000 years as shown in Fig. 5, in which the sum of the accumulated doses from all ²²⁶Ra and ²²⁸Ra series nuclei is calculated as a function of time. This is clearly less than ten times the half-life of ²²⁶Ra, which is 1600 years. As ²²⁶Ra decays, the dose rate gets lower and the accumulated dose increases only slightly. Considering the errors in estimating D_E, the age would not correctly be estimated for those more than 5000 or 6000 years old. High precision methods may become available in the future. Until then, when the ESR age appears to be older than 6000 years, it should be considered just to be older than 6000 years.

Fig. 5

The total of the accumulated dose as a function of time up to 10 ka. The accumulated dose saturates due to decay of ²²⁶Ra.

5. Conclusions

As results of simulation of the doses from the radioactive nuclei of ²²⁶Ra and ²²⁸Ra series, the contribution from ²²⁸Ra series can be significant for samples younger than 300 years. As for the present test sample, the contribution from ²²⁸Th to ²⁰⁸Pb was calculated to reach 60% at its maximum and to remain still 10% at 300 years. Currently, the ages for these samples without considering doses from ²²⁸Ra series would be overestimates. It is necessary to estimate the initial ²²⁸Ra concentration in barite in order to obtain the correct ages, and therefore, this is the further issue to be investigated especially for the samples older than 50 years old, in which ²²⁸Ra is not detected. Systematic investigations on the ²²⁸Ra/²²⁶Ra activity ratio in young or zero age samples would help estimate this value. The age limit of ESR dating of barite would be about 5000 to 6000 years due to decay of ²²⁶Ra, rather than the thermal stability of the signal.