. Introduction
Late Pleistocene marine terraces formed during interglacial sea-level highstands are widely distributed across the Japanese islands. Tephrochronology has been used to correlate these terraces with marine isotope stages (MIS) (Machida and Arai, 2003). Ages of marine terraces formed during the last interglacial (MIS 5e; 123 ± 7 ka) are well defined in many places (e.g., Koike and Machida, 2001) by widely distributed marker tephras. Marker tephras, such as Ontake Pm1 (On-Pm1, 95.7 ± 5.3 ka, Aoki et al., 2008) and Toya (106 ka, Shirai et al., 1997; 112–115 ka, Machida and Arai, 2003; 104 ± 15 ka to 118 ± 15 ka, Ganzawa and Ike, 2011) in eastern Japan, and Aso-4 (86.8–87.3 ka, Aoki, 2008) and Sanbe-Kisuki (SK, 100–115 ka, Shiraishi et al., 1992) in western Japan (Machida and Arai, 2003), have helped to establish the chronology of these MIS 5e terraces. However, marker tephras are not always found in marine terrace deposits; thus, the chronology of marine terraces has often been determined by counting interglacial deposits backward from MIS 5e. The dating of marine terraces is particularly important for evaluating long-term vertical crustal movements, and a suitable, universally applicable age determination method for this purpose is desirable.
Optically stimulated luminescence (OSL) dating of quartz has been widely applied to date coastal and marine sediments (Jacobs, 2008). In Japan, Tanaka et al. (1997) successfully used the multiple-aliquot additive dose (MAAD) method to determine a quartz OSL age for a marine terrace on the Noto Peninsula corresponding to MIS 5e. Barreto et al. (2002) also used the MAAD quartz OSL method to successfully date marine terraces in northeastern Brazil formed during MISs 7 and 5e. Choi et al. (2003) dated marine terrace sediments on the Korean Peninsula by using the quartz single-aliquot regenerative dose (SAR) method and obtained ages ranging from 50 ka to 70 ka, which are younger than the expected last interglacial age. The equivalent dose (De) of the OSL signal, however, is commonly close to saturation in samples from the last interglacial period, except when the environmental dose rate is low (Murray and Funder, 2003; Pawley et al., 2008; Pascucci et al., 2014). K-feldspar displays higher dose saturation levels than quartz, so the K-feldspar SAR method is suitable for dating older sediments. Pedoja et al. (2006a, 2006b) used the SAR method to obtain infrared stimulated luminescence (IRSL) ages of feldspar from marine terraces in Ecuador and Peru. Because luminescence signals of feldspars are known to decrease after burial as a result of tunneling (anomalous fading) (Aitken, 1985), they corrected their ages for fading following Huntley and Lamothe (2001) and obtained fading-corrected ages corresponding to MISs 5e, 7, and 9.
Thomsen et al. (2008) found that the IRSL signal measured at an elevated temperature of 225°C after an initial low-temperature IRSL measurement at 50°C (IR50; the subscript refers to the measurement temperature) is much more stable (fades less) than the IR50 signal. This signal is called a post-IR IRSL (pIRIR) signal; hereafter, the first and second stimulation temperatures are shown as a subscript (e.g., pIRIR50/225). The pIRIR method effectively minimizes anomalous fading and has been applied to the determination of depositional ages older than the limit of quartz OSL age (e.g., Buylaert et al., 2009; Thiel et al., 2010, 2015; Kars et al., 2012). Moreover, pIRIR signals obtained at the higher measurement temperature of 290°C (pIRIR50/290; Thiel et al., 2011a, 2011b, 2012; Buylaert et al., 2012, 2013, 2015) and multiple elevated temperature (MET) pIRIR signals obtained at measurement temperatures higher than 250°C (Li and Li, 2011, 2012; Li et al., 2014) have been found to be more stable and often do not require anomalous fading correction. Buylaert et al. (2012) and Roberts (2012) suggested that low fading rates (g-value: <1.0–1.5%/decade) may be an artifact of laboratory measurement, and that such rates may have a negligible effect on measured ages. Thiel et al. (2012, 2015) have used this sufficiently stable pIRIR50/290 signal to determine the ages of marine terrace deposits. Thiel et al. (2012) demonstrated the feasibility of using the pIRIR50/290 protocol to determine the ages of marine terrace deposits as old as MIS 13 in Tunisia. Thiel et al. (2011a) assumed that no fading correction of pIRIR50/290 signals from fine-grained polymineral samples from tephric loess in Japan was needed. Additionally, Zander and Hilgers (2013) reported that the pIRIR50/290 signal is stable enough for a dose estimation even as high as 1600 Gy, and they could determine ages as far back as the Brunhes-Matuyama reversal from fine polymineral grains from Lake El’gygytgyn, Siberia. Thiel et al. (2015) found that the pIRIR50/225 signal from coarse-grained K-feldspar from the Oga Peninsula, northeastern Japan, displayed a non-negligible fading rate (1.3–2.3%/decade), whereas Buylaert et al. (2012) showed that the pIRIR50/290 signal from the same material was sufficiently stable. Additionally, Thiel et al. (2015) showed that fading-corrected pIRIR50/225 ages (corrected using the approach of Huntley and Lamothe, 2001) and uncorrected pIRIR50/290 ages were consistent with one another and with independent age control.
In this study, we investigated pIRIR290 signals obtained after different first IR stimulation temperatures from K-feldspar from marine terrace deposits in northeastern Japan that formed during the last interglacial. For each different first IR stimulation temperature, we measured De values, dose recovery ratios, residual doses, and g-values, and then calculated fading-uncorrected and -corrected ages. To select the most suitable signal, we then compared the pIRIR ages with ages of the marine terrace MIS5e reported by Miyauchi (1987) and Koike and Machida (2001). The age of MIS 5e is based on Lisiecki and Raymo (2005) (123 ± 7 ka).
. Geological setting and sampling
Kamikita coastal plain
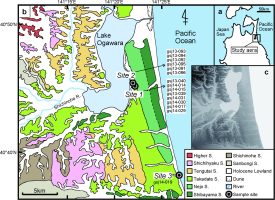
The Kamikita coastal plain, which lies along the Pacific coast at the northeastern end of Honshu Island, is about 50 km long and 30 km wide (Fig. 1). The plain has six marine terrace surfaces, named the Higher (Fukuromachi) (elevation, 110–220 m), Shichihyaku (90–110 m), Tengutai (45–80 m), Takadate (30–40 m), Nejo (10–15 m), and Shibayama (<10 m) surfaces, and two levels of fluvial terraces, the Shichinohe and Sanbongi (<5 m) surfaces (Miyauchi, 1985, 1987; Koike and Machida, 2001). The northeastern part of the Kamikita plain is occupied by Lake Ogawara, an irregularly shaped body of water that is generally elongated parallel to the coast. Seaward of the lake, only the Takadate terrace and the two fluvial terraces have been mapped. The Holocene plain is distributed only along the rivers draining into the lake and the lake’s outlet to the sea, and is not extensively developed along the modern shoreline.
Fig. 1
(a) Location map of the Kamikita coastal plain, northeastern Japan. (b) Map showing the distribution of Late and Middle Pleistocene marine terraces and sampling sites (after Miyauchi, 1985, 1987). In the legend, surface is abbreviated a “S” The elevation range of each terrace is given in the text. (c) Digital elevation model of the Kamikita coastal plain based on 10-m-grid data from the Geospatial Information Authority of Japan. Lighter grays indicate lower elevations, and darker grays and black indicate higher elevations.
The age of the Takadate terrace is constrained by the presence of the Toya tephra, which has been dated to 112–115 ka by a combination of fission track dating, thermoluminescence (TL) dating, and stratigraphy (Machida and Arai, 2003), and to 104 ± 15 to 118 ± 15 ka by red TL dating (Ganzawa and Ike, 2011). Shirai et al. (1997) and Matsuura et al. (2014) reported that based on marine sediment core the Toya tephra was erupted during MIS 5d (106 ka). The Toya tephra is found in the terrigenous upper part of the Takadate terrace deposits; thus, the underlying subtidal facies deposits are thought to have formed during the last interglacial sea-level high-stand (123 ± 7 ka). Although their ages are less well constrained, the Higher, Shichihyaku, and Tengutai terraces are presumed to have formed during older interglacial highstands, MIS 11, 9, and 7, respectively, whereas the Nejo (MIS 5c) and Shibayama (MIS 5a) terraces are younger than the Takadate terrace. Kuwabara (2009) correlated the Shichihyaku and Tengutai terraces with MIS 9 and 7, respectively, on the basis of phytolith evidence. The terrace sequence is thought to reflect both global sea-level changes and steady tectonic regional uplift caused by east–west horizontal compression during the Late Pleistocene (e.g., Miyauchi, 1985, 1987).
Outcrops and sampling
We investigated two outcrops (sites 1 and 2) at the landward edge of the Takadate terrace, facing Lake Ogawara (Fig. 1). Depositional facies of the outcrops were defined and interpreted based on sedimentary structures and grain size. The elevations of the facies boundaries were measured with a virtual reference station GPS (Leica Viva GS08plus, Leica). These outcrops are 330 m apart and appear to expose laterally continuous deposits. The depositional succession beneath the Takadate terrace consists of lower subtidal facies and an upper terrigenous deposit, both of which were sampled. Light-tight black PVC tubes 15 cm long and 5 cm in diameter were hammered into the outcrop to sample sediment unexposed to light. Modern beach sand (sample gsj14-019) was collected at site 3 (Fig. 1) to determine the residual dose. This sample was obtained from ca. 10 cm depth by using the same type of tube.
Site 1
The subtidal facies at site 1 consists of fine to coarse sand containing granules and pebbles (Fig. 2). The lower part of the unit, 8 m thick, consists of cross-laminated gravelly coarse sand alternating with cross-laminated fine to medium sand. The coarse sand contains wave dunes and the fine sand contains burrows. This assemblage reflects the dominance of storm-wave sedimentation in the lower shoreface (Walker and Plint, 1992; Cummings et al., 2009). The upper part of the unit, 2.5 m thick, is composed of trough cross-laminated coarse sand containing granules and pebbles, and it overlies the lower part of the unit with an erosional contact. The cross-lamination is indicative of the sedimentation of dunes in the upper shoreface (Clifton, 2006). The generally coarsening-upward succession in the shallow-marine unit thus consists of regressive shoreface deposits (Walker and Plint, 1992). The erosional upper boundary of the unit at 19.8 m elevation implies that overlying deposits were removed from the upper shoreface and foreshore by erosion.
Fig. 2
Columnar sections from sites 1 and 2. Grain size is categorized into clay, silt, very fine sand, fine sand, medium sand, coarse sand, very coarse sand, granules, and pebbles (C, Si, vfs, fs, ms, cs, vcs, G, and P, respectively). The bold horizontal line represents the erosional surface between the terrestrial and subtidal facies deposits. T.P. (Tokyo Peil) is the standard datum for elevation measurements in Japan.
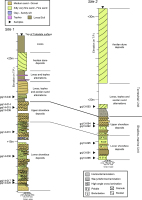
The terrigenous unit at site 1 consists of alternating sand and brownish silt. The silt layers are poorly sorted and contain sand and granules, and their brownish color indicates that they are loess beds or paleosols. A few unidentified tephra layers are intercalated with the silt layers. The sand layers are 30 cm to 200 cm thick and characterized by well-defined cross- to horizontal laminations. A 2-m-thick sand layer in the upper part of the unit exhibits aeolian dune stratification dipping eastward in the direction of the winter monsoon winds in this region. Other sand layers also probably represent aeolian dunes or sand sheets, because they are interbedded with paleosols.
We took four sediment samples for luminescence dating from different levels of the lower shoreface deposits (gsj14-017, gsj14-029, gsj14-030, and gsj14-031), three samples from one level of the upper shoreface deposits (gsj13-039, gsj14-014, and gsj14-015), and one sample from aeolian sand deposits (gsj13-040).
Site 2
The subtidal facies at site 2 consists of coarsening-upward regressive shoreface deposits similar to those at site 1. Its erosional upper boundary is at 18.0 m elevation, suggesting slightly deeper erosion than at site 1. The terrigenous unit, as at site 1, is composed of aeolian sand and brownish paleosols, but its uppermost part is dominated by 9-m-thick aeolian dune deposits showing east-dipping cross-lamination. The same aeolian dune extends along the eastern shoreline of Lake Ogawara (Fig. 1; Miyauchi, 1985, 1987).
Samples for luminescence dating were taken from three levels of the lower shoreface deposits (gsj13-091, gsj13-095, and gsj13-096), from two levels of the upper shoreface deposits (gsj13-092 and gsj13-094), and from one level of the aeolian sand deposits (gsj13-093).
Expected age of subtidal facies deposits
The two subtidal facies, upper shoreface and lower shoreface, accumulated under different water depths and during different time periods and thus have different sedimentation ages. In Denmark, Fruergaard et al. (2015) confirmed that samples from subtidal facies are completely bleached by using OSL ages of Holocene samples, which increase with depth in direct correspondence to the sedimentation age of each sample. During the Holocene, the sedimentation rate of beach shorefaces has been rapid, with sedimentary successions 10–15 m thick forming in only 2000 years (e.g., Tamura et al., 2007). On longer Pleistocene timescales (e.g., 100 ka), a 2000-year age difference comprises only 2% of a sample’s age. Thiel et al. (2015) illustrated a depth profile of pIRIR50/225 ages of samples from subtidal facies (Thiel et al., 2015; their Fig. 13); in this profile, the pIRIR50/225 ages of samples from subtidal facies collected at heights 5 m to 25 m do not increase with depth. Therefore, we do not expect the ages of our samples from the subtidal facies to increase with depth but to concentrate at about 123 ± 7 ka, the age of the MIS 5e sea-level highstand.
. Sample preparation, measurement apparatus, and dose-rate calculation
All samples were processed and measured at the luminescence laboratory of the Geological Survey of Japan. Sediment within 3 cm from each end of the tube, which may have been exposed to sunlight during sampling, was removed and used for measuring moisture content and dosimetry. The remaining sediment was processed to extract coarse grains of K-rich feldspar. The samples were treated with 10% HCl and 10% H2O2 to dissolve carbonate and organic matter, respectively, and then screened using 180 μm and 250 μm mesh sieves. Finally, the K-rich feldspar fraction (ρ = 2.53–2.58 g/cm3; Aitken, 1998) was isolated by using sodium polytungstate. The feldspar grains were then mounted in aliquots with a diameter of 8.0 mm by using silicone oil on stainless steel disks with a diameter of 9.8 mm.
Luminescence signals were measured with a TL-DA-20 automated Risø reader equipped with infrared LEDs for stimulation (145 mW/cm2; central wavelength, 870 nm) and a 90Sr/90Y beta source (dose rate, ca. 0.19 Gy/s) for laboratory irradiation, which was calibrated by using stainless steel and 180-250 μm calibration quartz from Risø. Emissions in the blue–violet region, which are dominantly K-feldspar emissions (Huntley et al., 1991), were measured through Schott BG3 (thickness, 3 mm), BG39 (2 mm), and GG400 (3 mm) filters.
The contributions of natural radioisotopes and cosmic radiation were considered in the determination of the annual dose rate. After mixing and homogenization of the dried sample, radioisotope concentrations were measured by inductively coupled plasma mass spectrometry and converted to dose rates by using the conversion factors of Guérin et al. (2011) (Table 1). The uncertainty of the radioisotope concentrations was assumed to be ±5%. Water content was estimated from the mean of the natural and saturated water contents and expressed as weight of water / weight of dry sediment, with a ±5% uncertainty. The saturated water content of 31.0% was calculated from the mean saturated water content of four samples (gsj13-039, gsj13-040, gsj13-093, and gsj13-094) and used for all samples. The α-dose and β-dose attenuation factors were taken from Bell (1980) and Mejdahl (1979), respectively. The relative alpha efficiency (a-value) of K-rich feldspar was set to 0.15 ± 0.05, as assumed by Balescu and Lamothe (1994). The size of the K-feldspar grains was determined to be 221 ± 6 pm by a CAMSIZER apparatus (Retsch Technology). The K content of the feldspar was assumed to be 12.5 ± 0.5% (Huntley and Baril, 1997). The internal U and Th contents were assumed to be zero. No internal α-dose rate contribution from U and Th was considered, referred to the data set shown in Duller (1992). The cosmic dose rate was estimated following Prescott and Hutton (1994).
Table 1
Radioisotope concentration, water content, cosmic ray and dose-rate for sediment samples. Listed water content was natural value. The water content for dose rate calculation was estimated from the mean of natural and saturated (31.0%) water contents. For details see main text.
. Uminescence characteristics
Equivalent dose measurement and procedural tests
Using gsj13-039 and gsj13-094, we investigated the characteristics of pIRIR290 signals with different first IR stimulation temperatures. The pIRIR stimulation temperature and preheat temperature were fixed at 290°C and 320°C, while the first IR stimulation temperature was varied between 50°C and 250°C with a 50°C increment. The luminescence signal was measured in 0.1-s bins. The decay curves of the five plRIR signals from gsj13-039 are shown in Fig. 3a. The highest intensity was that of the pIRIR50/290 signal at ca. 11,000 counts in the first 0.1 s, while the pIRIR250/290 signal intensity was only ca. 400 counts in the first 0.1 s.
Fig. 3
pIRIR signal characteristics of samples gsj13-039 and gsj13-094 with different first IR stimulation temperatures. The pIRIR stimulation and preheat temperatures were fixed at 290 and 320°C, respectively. (a) Typical signal intensities of pIRIR290 signals from sample gsjl3-039, (b) first IR stimulation temperature plateau, and (c) dose recovery ratio and residual dose after bleaching for 3 h with different first stimulation temperatures. The error bars show one standard error. In (b), the bold and dashed lines represent the average De of each sample, except for De at the first IR measurement temperature of 250°C for gsj13-039. In (c), the dashed lines represent the ±10% range.

Buylaert et al. (2012) performed a first IR stimulation temperature plateau test to check the dependency of pIRIR290 De values on the first stimulation temperature. Here, we also applied the pIRIR SAR protocol with different first stimulation temperature for our samples to determine De (Table 2; e.g., Buylaert et al., 2012; Yi et al., 2016). To construct a dose–response curve, the intensities were derived from the integral of the first 2.0 s (20 channels) after subtracting the average intensity during the last 20 s. The Analyst Version 4.31.9 (Duller, 2016) was used to calculate each De. The De at each stimulation temperature was determined by calculating the arithmetic mean and standard error of the aliquots (Fig. 3b). Most De values plotted around the average, except at the first IR stimulation temperature of 250°C for gsj13-039, which showed a large scatter.
Table 2
Single aliquot regenerative (SAR) protocol used for De measurements.
A dose recovery test was performed using at least six aliquots from each sample. Aliquots were exposed for 3 h to artificial sunlight in a UVACUBE 400 chamber (Hönle) with a SOL 500 lamp module at a lamp-to-sample distance of 50 cm. After this bleaching, half of the aliquots were given a dose of β-radiation nearly equal to each De value and then analyzed, and the remaining aliquots were directly measured to estimate the residual dose. These residual dose values were subtracted from the recovered doses. The arithmetic means of the dose recovery ratio and residual doses were calculated, and the uncertainty was represented as one standard error. The data are shown in Fig. 3c. The dose recovery ratios plotted within ±10% from unity, except at the first IR stimulation temperature of 250°C for gsj13-094.
Anomalous fading measurement
It has been suggested that the fading of the pIRIR290 signal is negligible in nature, because in very old samples measured by some studies the natural signal was close to the saturation level (Buylaert et al., 2011; Kars et al, 2012; Thiel et al., 2011b; Thomsen et al., 2011). Stability of the pIRIR290 signal has also been inferred from age comparisons with an independent age control (Thiel et al., 2011a; 2015; Zander and Hilgers, 2013). However, in these previous studies, the fading rates of the samples were around 1–1.5%/decade (Buylaert et al., 2012; Thiel et al., 2011b), and it was argued that the measured laboratory fading might be an artifact of the measurement procedure (Buylaert et al., 2012). On the other hand, Li and Li (2012) reported that the fading of the pIRIR50/290 signal was not negligible in their samples having a natural De range from 250 Gy to 700 Gy, but that fading of pIRIR200/290 signal was negligible.
In this study, we performed a fading test with different first IR stimulation temperatures using gsj13-039 and gsj13-094 to check the signal stability of our samples (Fig. 4). Additionally, for gsj13-040, gsj13-030, gsj13-093, and gsj13-095, we performed a fading test for pIRIR290 with first stimulation temperatures of 50°C and 200°C (Table 3). Our fading test protocol was based on Auclair et al. (2003). Following the dose (ca. 140 Gy) and preheating, the delay times were between 0.3 h and 96 h, and the g-values were calculated following Huntley and Lamothe (2001). To express the g-value, the arbitrary time (tc) was normalized to 2 days (g2days). The data consisted of about 10 points from each sample, and the uncertainty is reported as one standard error. An example is shown in Fig. 4a. For all samples, the g-values of the pIRIR,50/290 and pIRIR200/290 signals ranged from 1.25 ± 0.66%/decade to 2.53 ± 0.31%/decade and from - 1.34 ± 0.57%/decade to 1.57 ± 0.40%/decade, respectively. The g-values of the pIRIR50/290 signal were larger than those of the pIRIR200/290 signal. For other signals, most g-values decreased when the first IR stimulation temperature was higher (Fig. 4b). The data were also used to calculate the dimensionless recombination center density ρ’ (Huntley, 2006), summarized in Table 3 for the fading correction following Kars et al. (2008).
Fig. 4
Fading test results. (a) Typical results for sample gsj13-039; (b) g-values obtained with different first IR stimulation temperatures for gsj13-039 and gsj13-094. The error bars show one standard error.
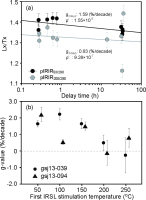
Table 3
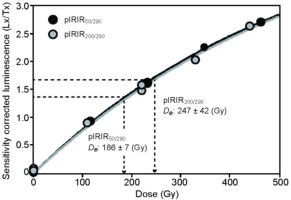
Results of pIRIR dating using different first IR stimulation temperatures. n is number of aliquots, ρ′ is the dimensionless recombination center density (Huntley, 2006). Residual dose was De after artificial sunlight bleaching for 3 h except for modern beach sand (gsj14-019) which was bleached for 800 h. Fading correction was performed based on Kars et al. (2008) and Kars and Wallinga (2009). To calculate the uncorrected ages, residual dose of modern beach sand (gsj14-019) was subtracted from De of each sample. D0 values were calculated based on Wintle and Murray (2006).
aTerrigenous sediments. bIf the average g-value of samples from site 2 was lower than zero, fading correction would not performed.
Residual dose estimation
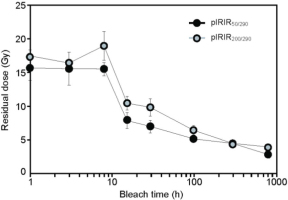
It is well known that the pIRIR signal is much more difficult to bleach than the IR50 signal (e.g., Buylaert et al., 2012; Kars et al., 2014; Sohbati et al., 2012). Additionally, Reimann et al. (2015) showed that different pIRIR stimulation temperatures have different rates of bleaching under daylight exposure. In bleaching experiments conducted by these previous studies, the pIRIR signal intensity did not reach an unbleachable residual level. However, Yi et al. (2016) recently showed that the residual dose of the pIRIR50/290 signal reached a lower limit after artificial sunlight (SOL2) bleaching for 300 h, and its residual dose was 6.2 ± 0.7 Gy. In this study, the De of the pIRIR50/290 signal of modern beach sand (gsj14-019) was 16 ± 2 Gy (Table 3), a much larger value than that of modern beach sand from Oga Peninsula (4.0 ± 0.2 Gy, Buylaert et al., 2012). Since the bleaching of gsj14-019 may have been incomplete, aliquots were bleached under artificial sunlight for longer than 300 h with a maximum bleaching time of 800 h. Sample aliquots were measured using the pIRIR50/290 and pIRIR200/290 protocols, and the residual dose at each bleaching time was calculated as the average of at least six aliquots with an uncertainty of one standard error (Fig. 5). The pIRIR50/290 and pIRIR200/290 De values before bleaching, which were 15.7 ± 1.8 and 17.3 ± 1.0 Gy, respectively, decreased to 2.8 ± 0.2 and 3.9 ± 0.2 Gy, respectively, after 800 h of bleaching. These remaining De values were assumed to be the unbleachable residual doses, and they were subtracted from all De values used to calculate the pIRIR50/290 and pIRIR200/290 ages (Table 3). For other signals, residual doses after 3 h of bleaching in the dose recovery test increased with the first IR stimulation temperature (Fig. 3c). This result indicates that the bleachability of the pIRIR290 signal decreases as the first stimulation temperature increases. Therefore, the residual doses of the pIRIR100/290, pIRIR150/290, and pIRIR250/290 signals were inferred by linear interpolation and extrapolation of the pIRIR50/290 and pIRIR200/290 signals. The assumed residual doses and errors of the pIRIR100/290, pIRIR150/290, and pIRIR250/290 signals were 3.2 ± 0.2, 3.5 ± 0.2, and 4.3 ± 0.2 Gy, respectively.
. Ages and discussion
Fading-uncorrected (residual-subtracted) ages
The fading uncorrected ages obtained with different first IR stimulation temperatures from gsj13-039 and gsj13-094 are shown in Fig. 6a and Table 3, and those of the pIRIR50/290 and pIRIR200/290 signals from the samples from the subtidal facies deposits are shown in Fig. 7. The uncorrected ages of gsj13-039 with different first IR stimulation temperatures are generally consistent with the expected age (MIS 5e, 123 ± 7 ka), with a possible exception of the pIRIR50/290 signal (Fig. 6a). On the other hand, the uncorrected gsj13-094 ages of pIRIR100/290, pIRIR150/290 and pIRIR250/290 signals are slightly older than the expected age if we do not consider the large scatter of own age. The uncorrected ages of the pIRIR200/290 signals of all samples (Fig. 7) were concordant with the expected age. The uncorrected ages of the pIRIR50/290 signal from the samples from site 2 were also concordant with the expected age, but the ages of the pIRIR50/290 signal from four samples from site 1 were underestimated.
Fig. 6
(a) Uncorrected and (b) corrected pIRIR ages of gsj13-039 and gsj13-094 obtained with different first IR stimulation temperatures. The error bars show one standard error.
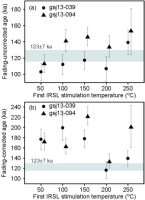
Fig. 7
Columnar sections as in Fig. 2. For sites 1 and 2, the fading-uncorrected and -corrected ages of the PIRIR50/290 and PIRIR200/290 signals are shown with one standard error. For site 2, the fading corrected ages of PIRIR200/290 signals were not calculated because the average ρ’ value was lower than zero. For each site, the vertical gray bar shows the expected age range. T.P. (Tokyo Peil) is the standard datum for elevation measurements in Japan.

Fading-corrected (residual-subtracted) ages
In the previous section, we showed that fading rates of the pIRIR50/290 signal were positive in all samples whereas the fading rates of the pIRIR200/290 signal were smaller and consistent with zero in four samples (taking account of the 2-σ uncertainty).
To apply the fading correction, it is necessary to consider the shape of the dose–response curve. If a De value is within a linear region of the curve, the method of Huntley and Lamothe (2001) can be applied, but if it is on a non-linear part, the method of Kars et al. (2008) must be applied. For our samples, all natural signal to natural test dose (Ln/Tn) ratios lay on a non-linear part of the dose–response curve (Fig. 8). Therefore, the fading correction was performed by the method of Kars et al. (2008) and Kars and Wallinga (2009). This fading correction methods is based on the model of the quantum-mechanical tunnelling process proposed by Huntley (2006). The fading-corrected ages were calculated by plotting measured Ln/Tn on the modelled growth curve, which was obtained from the measured dose–response curve, the the dimensionless recombination center density ρ’, and the dose rate. The dimensionless value ρ’ was calculated by fitting equation (7) of Huntley (2006) to the fading test results. The attempt-to-escape frequency s was fixed at 3 × 1015 s–1 following Huntley (2006). In the fading tests of gsj13-039 and gsj13-094 with different first IR stimulation temperatures, ρ’ ranged from (–0.42 ± 1.15) × 10–6 to (2.22 ± 0.33) × 10–6 and from (–0.20 ± 0.76) × 10–6 to (2.24 ± 0.40) × 10–6, respectively. To calculate the fading-corrected ages of the pIRIR50/290 and pIRIR200/290 signals, the average value of ρ’ was used for each sampling site: (2.12 ± 0.26) × 10–6 and (0.34 ± 0.75) × 10–6, respectively, for site 1 (gsj13-040, gsj13-039 and gsj14-030), and (1.76 ± 0.30) × 10–6 and (–0.02 ± 0.79)× 10–6, respectively, for site 2 (gsj13-093, gsj13-094 and gsj13-095). For the pIRIR100/290, pIRIR150/290, and pIRIR250/290 signals, the ρ’ values of gsj13-039 and gsj13-094 were used for the fading correction.
The corrected ages are shown in the same way as the uncorrected ages (Figs. 6b and 7). Except for the pIRIR200/290 signals, the corrected ages with different first IR stimulation temperatures overestimated the expected age. The corrected ages of the pIRIR200/290 signals of samples from site 1, like the uncorrected ages of the pIRIR200/290 signals of all samples, were concordant with the expected age (Fig. 7). On the other hand, the corrected ages of the pIRIR50/290 signals from all samples were always older than the expected age. The characteristic saturation dose (D0) values of our dose–response curves were calculated based on Wintle and Murray (2006) (Table 3). The resultant D0 values, generally ranging between 300 and 500 Gy, were lower than the D0 values of pIRIR50/225 and pIRIR50/290 signals reported by Li et al. (2017) (500-730 Gy), which were obtained from the dose response curve to the saturation level. Though the size of the regenerative doses in this study were adequate to estimate a reliable De value, these low 2D0 values were calculated from the dose–response curve which was not constructed up to saturation level. Therefore, to estimate a reliable corrected age of the pIRIR50/290 signal, the dose–response curve used for the fading correction should have been extended to saturation level.
Discussion
In this study, both fading-uncorrected and -corrected pIRIR200/290 ages in site 1 were shown to be in agreement with the expected age. When we compared the uncorrected and corrected pIRIR200/290 ages, the corrected ages showed a much narrower age cluster around the expected age of 123 ± 7 ka, presumably because of a small fading influence. We conclude that the fading-corrected pIRIR200/290 ages are most suitable, if a positive ρ’ value is calculated.
The fading-corrected and -uncorrected ages of the pIRIR200/290 signals of our terrigenous samples (gsj13-040 and gsj13-093) were 81 ± 8 ka and 86 ± 8 ka, respectively, whereas the corrected ages of the samples from the subtidal facies ranged from 116 ± 11 ka to 136 ± 15 ka. The field evidence showed that the terrigenous sediments accumulated after the deposition of the subtidal facies and were separated from them by an erosional surface. These ages indicate that the terrigenous sediment was deposited during MIS 5a. In the samples from the subtidal facies, we found no systematic stratigraphic trend of the pIRIR200/290 ages. This concentration of ages of the pIRIR200/290 signal is similar to previous results from the Oga Peninsula for the pIRIR50/225 signal (Thiel et al. 2015). The mean pIRIR200/290 ages from the subtidal facies of site 1 and site 2 were calculated to be 126 ± 3 ka and 132 ± 2 ka, respectively.
. Conclusion
The pIRIR dating protocol was applied to marine terrace deposits from the last interglacial on the Kamikita coastal plain, northeastern Japan. To calculate fading-uncorrected ages, the residual dose that was obtained by bleaching of a modern beach sample for 800 h in a solar simulator was subtracted from the De of each sample. With regard to the stability of the pIRIR signal, the g-values decrease as a function of first IR stimulation temperature; from 2%/decade at 50°C to near zero for the pIRIR200/290 and pIRIR250/290 signals. For site 1, the fading-corrected ages of the pIRIR200/290 signals showed a much narrower age cluster around the expected age of MIS 5e; the average corrected age (±1 standard error) was 126 ± 3 ka. On the other hand, for site 2, the fading correction was not necessary because the average ρ’ value was lower than zero and the signal was stable; the average uncorrected age was 132 ± 2 ka. We conclude that the pIRIR200/290 protocol is most suitable for determining reliable ages of marine terrace deposits of the Kamikita plain. This robust dating protocol can be further applied to determine the ages of not only terraces formed during substages of MIS5 (5a, 5c) but also those of older marine terraces, for which age evidence is limited.