. INTRODUCTION
In the trapped charge dating community, no matter what techniques and facilities are used, it is important to compare results between different laboratories to show they are all able to measure the same age for the same sample. Such intercomparisons have been well carried out in radiocarbon dating (Scott et al., 2010; Adolphi et al., 2013; Hajdas et al. 2017 and Jull et al., 2018), and cosmogenic dating (Vermeesch et al., 2015 and Blard et al., 2015). In luminescence dating, Murray et al. (2015) found significant discrepancies in the determination of dose rates in natural samples between more than 20 luminescence dating laboratories using various facilities. These included neutron activation analysis (NAA), inductively-coupled plasma mass spectrometry (ICP-MS), X-ray fluorescence (XRF), atomic absorption spectroscopy (AAS), thick source alpha counting (TSAC), and high resolution gamma spectrometry. Part of this large variability (RSD ∼12%) probably arises from the difficulties in homogenising and dissolving samples so that the <500 mg used in, e.g. ICP-MS and NAA is representative. High resolution gamma spectrometry offers an obvious advantage when a more representative and thus usually more accurate dose rate is the aim because it measures samples 100–1000 times larger; a homogenous and representative sample is thus much easier to prepare. However, the high capital cost and level of operator experience required for a reliable operation have hindered its wider application in luminescence dating laboratories.
In a recent preliminary study, Bu et al. (2018) showed that a NaI(Tl) scintillator-based gamma spectrometer is also able to determine burial dose rates accurately in natural geological samples, at a significantly lower cost. Using a 3″×3″ NaI(Tl) scintillation crystal, they reported minimum detection limits (MDLs) for 40K, 238U, and 232Th activity concentrations of 25, 4.8, and 2.5 Bq·kg−1, respectively. (MDL is defined here as the activity or activity concentration for which the random uncertainty is 30%, Bu et al., 2018). The above data were obtained using a count time of 20 hours, a 0.19 kg sample and an improved three-window spectrum analysis approach; for 0.23 kg sample used below, these values correspond to 21, 4.0 and 2.1 Bq·kg−1, respectively. Even though these MDLs are close to or below the lower limits found in most natural sediments, lower MDLs, especially for 238U and 232Th, are desirable to achieve a burial dose rate with lower uncertainty.
In this study, we investigate the potential of a different approach – full spectrum analysis (FSA) (Dean, 1964; Hendriks et al., 2001; Jeong et al., 2014) to reduce the MDLs. An iterative, reweighted least-squares (IRLS) regression (Burrus et al., 1994; Daubechies et al., 2010; Chen et al., 2018) is used to fit three calibration standard spectra (40K, 238U and 232Th series in equilibrium) to the unknown spectrum (after subtraction of an appropriate background). When compared to the three-window approach, FSA uses considerably more statistical information from each spectrum, and the additional degrees of freedom provide a direct estimate of uncertainties from the fitting process; this is in contrast to the uncertainties in a three-window analysis, which are based only on counting statistics. Here we investigate the benefits of the FSA approach. The revised MDLs are compared with those from both the three-window analysis of Bu et al. (2018) and high-resolution HPGe gamma spectrometry (Murray et al., 2018). We also measure 20 representative natural samples and compare the analyses with those from high resolution spectrometry. Finally, we discuss the precision and accuracy available from our NaI(Tl) gamma spectrometer, their dependence on counting time, and the relationship between activity concentration measurement uncertainties and those on dose rates.
. MATERIALS AND METHODOLOGY
Experimental setup
The configuration of the experimental setup used in this study is essentially the same as the one reported in Bu et al. 2018. Briefly, a 3″×3″ NaI(Tl) scintillation crystal (Harshaw) and photomultiplier tube (PMT) assembly is connected to a digital tube base (TB-5, Amptek); this contains all necessary electronics for the acquisition of gamma spectra. The entire detector (NaI(Tl) crystal, PMT and digital tube base) is contained within a 10 cm thick lead shield. DppMCA software from Amptek is used to acquire the gamma spectrum. In order to characterise the NaI(Tl) detector, and to evaluate its performance and the accuracy of the algorithm we employ for spectrum analysis (see below), samples were also measured using our standard high resolution HPGe gamma facility (Murray et al., 2018). Because the NaI(Tl) detector and the HPGe detector we used in this study have different dimensions, samples (finely ground sediment mixed with wax and cast in a cup-shape geometry) of different dimensions were prepared for counting on the two different detectors; in each case, these two cups were prepared simultaneously from the same homogenised sediment sample mixture. During data collection, temperatures at the top surface of the NaI(Tl) crystal and in the air in the lead shield were continuously measured by K-type thermocouples and monitored by a thermocouple data logger (USB TC-08, Pico Technology, UK).
Because of atmospheric 222Rn, there can be a correlation between background count rate and atmospheric pressure, season and room ventilation (Mentes and Eper-Pápai, 2015; Schubert et al., 2018). To minimise this effect, we have filled the cavity around the detector with polystyrene foam (Bu et al., 2018); this minimises the volume available to 222Rn contamination. Using this configuration, we have been unable to detect a significant change in background count rate in 6 measurements over a period of 33 weeks.
Sample preparation
All natural samples were ignited at 450°C for 24 hours (to determine organic content) before grinding to <200 μm, and then mixing with high viscosity wax (Bottle wax, blend 1944, British Wax Refining Company) on a hotplate at ∼80°C. A typical wax:sample mass ratio of ∼1:2 gives a typical sample mass of 250–300 g in the final counting geometry. Sample and calibration standards are cast in the same cup-shaped geometry, with a wall thickness of 10 mm, an internal diameter of 80 mm and an internal height of 60 mm. Samples are stored for >20 days before counting, to allow 222Rn to reach secular equilibrium with its parent 226Ra. Inverted, the sample cups are placed over the top of the NaI detector for counting. Murray et al. (2018) report that the dependence of self-attenuation on sample mass for all likely mixtures in the sample cup is <2% over the energy range of interest, i.e., from ∼160 keV to ∼2.87 MeV.
In order to prepare uranium and thorium calibration standards, the appropriate IAEA certified reference material BL-5 (7.09 ± 0.03% U, NRCAN-1) or OKA-2 (2.893 ± 0.058% Th, NRCAN-2) was diluted in low activity quartz-rich sand (M32, Sibelco Belgium; 226Ra 1.39 ± 0.08; 232Th 0.85 ± 0.06, 40K 6.8 ± 0.7 Bq·kg−1, measured by an HPGe gamma spectrometer), ground to <200 μm. The diluted reference materials were then mixed with wax to give individual parent activities of ∼800 Bq per cup. For potassium calibration standards, analytical grade K2SO4 (14.20 Bq·g−1 assuming stoichiometry, purity given by the manufacturer as 100.4%) was mixed directly with wax to give ∼2700 Bq per cup. From the calculation, the expected uncertainties arising from the weighing process are <<1%. Three standards were prepared from separate dilutions for each radionuclide (named as K1-3, U1-3 and Th1-3, respectively). A background sample cup was prepared by casting pure wax. In order to correct for the gain drift caused by temperature changes during counting the algorithm described in Bu et al. (2018) employed a common reference spectrum containing all characteristic peaks from 40K, 238U and 232Th. This spectrum was derived from a mixed sample of 40K, 238U and 232Th (named KUTh reference), prepared by diluting BL-5 and OKA-2 in K2SO4 to give a sample cup containing ∼2700 Bq of 40K and ∼70 Bq of 238U and 232Th, respectively. The activity ratios of the three nuclides in this KUTh reference sample are chosen to be similar to the average ratio of 40K, 238U and 232Th activities in natural geological samples (e.g., Ankjærgaard and Murray, 2007 and references therein).
Because our NaI(Tl) scintillation detector is insensitive to low energy photons, photons emitted by 222Rn short-lived daughters dominate the U-series spectrum; given secular equilibrium between 222Rn and 226Ra (ensured by casting in wax and storing), our U analyses are actually 226Ra analyses.
Spectrum drift correction
The full spectrum analysis algorithm used in this study requires considerably more stringent energy stability across the entire spectrum than does the three-window algorithm. After the measurement, spectra from unknown samples, and background and 40K, 238U and 232Th calibration standards were all energy corrected to the common reference spectrum from the KUTh reference sample before spectrum analysis. The linear correction algorithm (with an intercept) corrects two specific peaks in each spectrum to the two corresponding peaks in the reference spectrum. The correction algorithm is described in Bu et al. (2018), but we have now improved the selection of the correction reference peaks, especially for correction of 40K calibration standard spectra (in which other peaks are only derived from the background, and so are poorly defined).
The gamma spectra from the background, 40K, 238U and 232Th calibration standards and unknown natural samples all have characteristic peaks of very different absolute and relative intensities; as a result, the most useful reference peaks are dependent on the spectrum to be drift corrected. For example, natural samples usually contain significant activity concentrations of 40K, 238U and 232Th, and so drift correction employs the ubiquitous ∼85 keV peak (X-ray) from U and Th, and the 1.46 MeV gamma-ray peak from 40K. The same is true of background spectra although all the intensities are, of course, much weaker. However, this choice is impractical when we select reference peaks for the gamma spectra from calibration standards, e.g., in the 40K standard spectrum, the X-ray peak is not detectable, and so the 1.46 MeV from 40K emission and its Compton backscatter peak (measured at 226 keV) are used. This is in contrast to the more conventional choice of Bu et al. (2018), where the 1.46 MeV peak (40K) and the background 2.61 MeV peak from the 232Th series were employed. We now prefer the backscattered peak because the background 2.61 MeV peak is too weak to allow accurate determination of the peak centroid. For the 238U and 232Th calibration standards, we selected the same peaks as those described in Bu et al. (2018), i.e., for the 238U calibration standard with negligible 40K, we employ the X-ray peak and the 214Bi peak (1.76 MeV, U series); for 232Th calibration standard, we use the X-ray peak and the 208Tl peak (2.61 MeV).
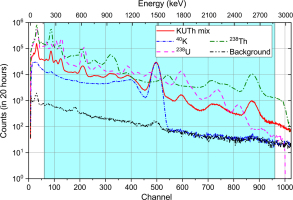
Fig. 1 illustrates an example of all corrected spectra from one set of 40K, 238U and 232Th calibration standards, a corrected background spectrum, and the KUTh mixed reference spectrum used for drift correction. The shaded region in Fig. 1 shows the region of interest (ROI) for the full spectrum analysis; this is discussed in more detail in Section 2 – Full spectrum analysis and calculation of activity.
Calibration of detection efficiency
Cups from all three sets of 40K, 238U and 232Th calibration standards (9 in total) were each counted for 20 h, then each spectrum was drift corrected to the reference spectrum, and normalised to counting time to give the count rate in each channel (counts·ks−1). The background was counted three times (each for 20 h); after correction and normalisation, these three spectra were averaged. This averaged background spectrum was then subtracted from each 40K, 238U and 232Th normalised spectrum. The detection efficiency (counts·ks−1·Bq−1) of each nuclide was derived by dividing the count rate in each channel with the known activity (Bq). Finally, the detection efficiencies resulting from three standard spectra were averaged to reduce the contribution to scatter resulting from manufacturing (mainly dilution and casting) of the calibration standards.
Full-spectrum analysis and calculation of activity
In FSA, the shape of a large part of the sample spectrum is analysed, and decomposed to determine the contributions from the three individual 40K, 238U and 232Th standard spectra and the background spectrum. The counts in the first prominent peak (as shown in Fig. 1) are mostly X-ray emissions (from U and Th), while the counts above the 2.61 MeV peak are mostly from cosmic rays; these two energy peaks (∼85 keV and 2.61 MeV) provide limits to the range of energies employed in the FSA. Here, we select a region of interest (ROI) from channel 70 to 960 (in total M = 891 channels), corresponding to an energy region from ∼160 keV to ∼2.87 MeV.
Formalising the above, in each channel, the measured unknown sample spectrum S is made up of the sum of the 40K, 238U and 232Th detection efficiencies DEk (k=1, 2, 3), each multiplied by the activity Ak contained in the unknown sample, plus an averaged background spectrum (Bg), i.e.:
As we know the total number of channels in the energy range of interest is M, in Eq. 2.1, there are then M linear equations in total with three unknown variables Ak (k=1, 2, 3). We use least-square linear regression to estimate the 40K, 238U and 232Th activities by minimising the chi-squared:
After obtaining the first estimate of the activities Ak,0, the estimation accuracy is improved by a second least-squares linear regression following the inclusion of a weight factor W(i) into Eq. 2.2:
In Eq. 2.3, instead of employing the weight factor W(i) = S(i) as described in Hendriks et al. (2001), or as a more complicated form involving estimated activities and uncertainties on all relevant spectra (Jeong et al., 2014), we simply use the absolute value of the fitting error in each channel generated in the previous step as the weight factor W(i).
In this way, those channels with a higher fitting error have a higher weight factor, giving a faster convergence. We carried out this process iteratively by continuously using a newly obtained W(i) in the current step (defined as step n) as the weight factor for the next step (step n+1) of chi-squared minimisation, until the changes in all of the estimated activities reach the condition:
This process delivers a fitting error contribution of ∼0.001 Bq·kg−1 for a typical >100 g sample.
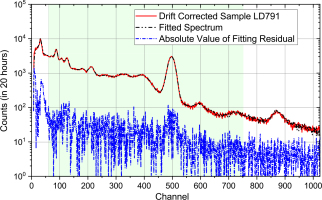
Fig. 2 shows an example using the natural sample (LD791); the original sample spectrum and the fitted spectrum overlap can be seen to agree very well over the entire energy range; the weak structure visible in the residuals presumably arises from errors in the drift corrections.
Uncertainty analysis
The uncertainty analysis on the burial dose rate of natural samples is not a trivial task; there are many sources of uncertainty, both correlated and uncorrelated, contributing to the final propagated uncertainty on the burial dose rate. In this study, as usual, we categorise them into systematic and random uncertainties. The systematic uncertainties depend mainly on the standards we use to calibrate the 40K, 238U and 232Th detection efficiencies on our NaI gamma detector. The random uncertainty includes the uncertainties contributed by the finite counts in each channel (counting statistics) and the fitting uncertainty arising from the fitting algorithm used to determine the activity concentrations. The details of the derivation of systematic and random uncertainties are summarised in the Supplementary Material.
Determination of dose rate
Once the activity concentrations of 40K, 238U and 232Th in the unknown sample are determined, we derive beta and gamma dose rates based on the dose rate conversion factors published by Guérin et al. (2011) and Liritzis et al. (2013). In addition, we updated various parameters including the atomic weights, abundances and decay constants (and their uncertainties) of 40K, and all U and Th decay series from the IAEA (IAEA Live Chart of Nuclides, March 2018). The revised activity concentrations per ppm are listed in Table 1. In order to determine the uncertainties in beta and gamma dose rates, updated uncertainties of all relevant quantities, e.g., half-lives, energies, branching ratios, atomic weights, atomic abundances etc., were taken into account and combined during the error propagation process.
Table 1
Updated 40K, 238U and 232Th activity concentration per ppm for dose rate derivation.
| Radionuclide | Activity concentration (Bq·kg−1) | Uncertainty (Bq·kg−1) |
|---|---|---|
| 40K | 317 | 3 |
| 238U | 12.922 | 0.025 |
| 232Th | 4.061 | 0.029 |
During the derivation of field beta and gamma dose rates, radon loss in the field is assumed to be 20% ± 10%; this is the default assumption used in our laboratory. In addition, we assume 226Ra to be in equilibrium with its series parent 238U. Both these assumptions can be varied on a site-specific basis.
The total dry burial dose rate was then calculated by summing the beta and gamma dose rates. Since the activity concentrations of the 238U and 232Th daughter nuclides are all dependent on activity concentrations of 238U and 232Th, respectively, the contributions from their individual uncertainties to the total beta or gamma uncertainties are correlated. In addition, beta and gamma dose rates are also correlated because they are all derived from the same 40K, 238U and 232Th activity concentrations. During the summing of beta and gamma dose rates, propagation of these correlated uncertainties are handled by the uncertainty analysis tool Metas.UncLib (Zeier et al., 2012), in the same manner as the uncertainties for the activities (see Supplementary Material).
. RESULTS AND DISCUSSION
Minimum detection limits (MDLs)
MDLs for 40K, 238U and 232Th activities (or activity concentrations for a sample with a certain weight) are one of the most important specifications of a gamma spectrometer intended for the measurement of dose rates. In this study, we used the same procedures as described in Bu et al. (2018) to measure these MDLs experimentally. In short, we measured the same KUTh mixed sample cup for ten various lengths of time t: 30, 60, 120, 300, 600, 1200, 2400, 4500, 9000 and 72000 s. The background cup was counted for 72000, 71970, 71940, 71880, 71700, 71400, 70800, 69600, 67500, 63000 s. After drift correction, we combine a sample spectrum (e.g. that counted for 30 s) with the corresponding background spectrum (in this case, that counted for 71970 s) to give a spectrum corresponding to a total effective counting time of 72000 s (20 hours). This gives us in total ten synthesised spectra equivalent to those that would have been obtained from ten samples of well-known relative activity concentrations; all counted for 20 h. The expected activity concentration (AEXP) corresponding to the counting time t of each synthesised sample was calculated from the activity concentration measured for 20 h (AMEAS_20h):
These ten synthesised sample spectra were analysed by FSA and the apparent 40K, 238U and 232Th activities (AMEAS) derived. Here we define the MDL as the value of AEXP expected to have a corresponding random uncertainty of 30% on AMEAS. Fig. 3a–3c summarises the FSA analysis results, and gives MDLs for 40K, 238U and 232Th activities of 1.1, 0.09 and 0.07 Bq, respectively. By dividing by the maximum practical sample mass in our cup geometry (0.23 kg), the corresponding MDLs on activity concentrations for 40K, 238U and 232Th are 4.8, 0.4 and 0.3 Bq·kg−1, respectively. Table 2 compares these FSA MDLs with those from the three-window approach (Bu et al., 2018) from a NaI(Tl) spectrometer, and MDLs from a high resolution HPGe gamma spectrometer (Murray et al., 2018). Table 2 shows FSA MDLs are one order of magnitude lower than those achieved by three-window spectrum analysis, and are one order of magnitude higher than those from an HPGe detector. This indicates the FSA approach is a significant improvement on the results obtainable from a low resolution NaI(Tl) gamma spectrometer, presumably because of much greater statistical precision. The total number of counts recorded in the energy region of interest in FSA is orders of magnitude greater than that in the windows-of-interest in the three-window approach; the FSA approach makes use of almost all statistical information contained in the sample spectrum.
Fig. 3
(a–c) Minimum detection limits (MDLs) for activities of 40K, 238U and 232Th, respectively, defined as random uncertainty approaching 30%, when random uncertainty is expressed as a function of expected activity (AEXP); (d–f) Comparison of measured 40K, 238U and 232Th activity concentration (AMEAS) and expected activity concentration (AEXP), showing the accuracy of measurement and FSA analysis. The error bars in panels (d-f) shows the random uncertainty.
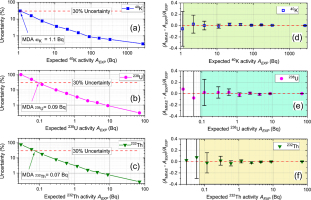
Table 2
Comparison of MDLs (Bq·kg−1) from different studies.
| Nuclide | NaI(Tl) spectrometer (Sample weight: 0.23 kg) | HPGe spectrometer (Sample weight: 0.25 kg) | |
|---|---|---|---|
| FSA (This study) | 3-Window (Bu et al., 2018) | (Murray et al., 2018) | |
| 40K | 4.8 | 21 | 0.6 |
| 238U | 0.4 | 4.0 | 0.04 |
| 232Th | 0.3 | 2.1 | 0.03 |
Measurement accuracy and precision
The accuracy of the measurement and analyses can be examined in Fig. 3d–3f, in which the shaded regions in all three subpanels represent the activity ranges above MDLs, for 40K, 238U and 232Th, respectively. The deviations AMEAS – AEXP between the measured and expected activities for 40K, 238U and 232Th, are normalised to the expected activity AEXP, as shown in Fig. 3d–3f, as a function of AEXP. The error bars shown in Fig. 3d–3f are derived from the random uncertainties of the expected and measured activities. Within these shaded regions, 40K, 238U, and 232Th analyses are all consistent with the expected results, without any obvious systematic error, even when the expected activities approach the MDLs.
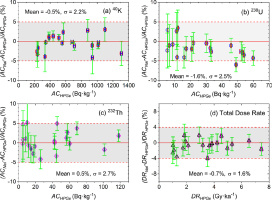
The precision and accuracy of the FSA algorithm were further evaluated by comparison of our analyses with those from a high resolution HPGe spectrometry facility (Murray et al., 2018; making the same assumptions concerning secular equilibrium), using 20 natural samples covering a range of activity concentrations. Fig. 4a–4c shows the deviation ACNaI – ACHPGe between activity concentrations obtained from the NaI(Tl) spectrometer and those from the HPGe spectrometer are normalised to ACHPGe. The resulting dry dose rates for all 20 unknown samples are normalised in the same manner, and the normalised deviations are compared in Fig. 4d.
Fig. 4
Normalized deviations between those activity concentrations for 40K, 238U and 232Th (a–c), and total (β + γ) dose rates (d) determined by the NaI(Tl) spectrometer and those determined by an HPGe spectrometer, for 20 geological samples. The shaded regions represent ±5% deviation in panels (a–c), and ±4% deviation in panel (d). The standard deviation for 20 data in each subpanel show a high measurement precision on NaI(Tl) spectrometer. All error bars in panel (a-c) and in panel (d) are derived from the total uncertainties of ACNaI and ACHPGe, and total uncertainties of DRNaI and DRHPGe, respectively.
In this study, all unknown samples, 40K, 238U and 232Th calibration standard cups, mixed KUTh reference cup for drift correction and background cup were measured at a room temperature of ∼20–25°C for 20 hours. The maximum temperature drift during each measurement was ∼0.4°C.
As shown in Fig. 4a–4c, almost all normalised deviations (ACNaI – ACHPGe)/ACHPGe of 40K, 238U and 232Th for 20 samples lie within the shaded region of ±5%, with only one data point below −5% line in 238U panel and another two just above +5% line in 232Th panel. For the total beta and gamma dose rates (Fig. 4d), normalised deviations (DRNaI – DRHPGe)/DRHPGe lie within the shaded region (±4%) for all 20 studied samples. The standard deviations (n=20) on these ratios are also listed in each subpanel in Fig. 4. All activity concentration ratios have a standard deviation of <3%, and the corresponding variability in dose rates is <2%.
In addition, Fig. 4a–4d show that there is no suggestion of a systematic deviation, either in the activity concentrations or in the total dry beta and gamma dose rates. This is also indicated in Table 3 by the average ratios of ACNaI/ACHPGe and DRNaI/DRHPGe, with low standard deviations (n = 20) of 0.4 to 0.6%.
Counting time
Another important consideration when using a gamma spectrometer for measuring dose rates in OSL dating applications is the counting time. The required count time is dictated by the required dose rate uncertainty and the sample activity. As discussed above, the total uncertainty on dose rate is mainly derived from random and systematic uncertainty in 40K, 238U and 232Th activity concentrations. While the systematic uncertainty is fixed (at ∼2%), the random uncertainty, no matter whether from the fitting error of FSA algorithm or from counting statistics, is mainly determined by the counts in each channel.
Quantitative investigation of the dependency on counting time was carried out by counting the same natural sample (LD962) for different lengths of time, i.e., 5, 10, 20, 30 min, and 1, 2, 5, 10, 20 hours. Fig. 5a–5c and (d) show the dependence of the measured activity concentrations of 40K, 238U and 232Th, and total beta and gamma dose rates, respectively, on counting time. The results are compared with those measured on the HPGe spectrometer for 20 hours, i.e., 235, 8.6, and 8.3 Bq·kg−1 for activity concentrations of 40K, 238U and 232Th and 1.09 Gy·ka−1 for total dose rate; these values are represented by the thick horizontal dashed lines in each sub-panel in Fig. 5. The shaded region in each subpanel links to the right vertical axis and shows the dependence of the corresponding normalised deviations between the results from the NaI(Tl) spectrometer and the HPGe spectrometer for activity concentrations (ACNaI − ACHPGe)/ACHPGe (Fig. 5a–5c) and for corresponding derived dose rates (DRNaI − DRHPGe)/DRHPGe (Fig. 5d). These data indicate the counting times required to achieve a specified level of precision in the activity concentrations of 40K, 238U and 232Th and the derived dose rate, e.g. a 30 min count will lead to a ∼±10% uncertainty on dose rate.
Fig. 5
Activity concentrations (a-c) and total dose rate (d) of a natural sample (LD962) counted with different counting time on NaI(Tl spectrometer. The horizontal dashed line in the centre of shaded region in each subpanel represents the activity concentration (a-c) and total dose rate (d) from HPGe spectrometer. All error bars in panel (a-c) and in panel (d) denote the total uncertainties of ACNaI, and total uncertainties of DRNaI, respectively.
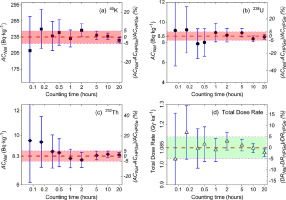
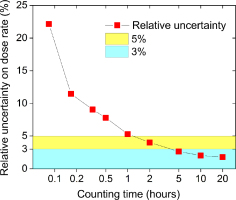
Fig. 6 shows the variation in the uncertainty on the total dose rate with the counting time, for a sample with 235, 8.6, and 8.3 Bq·kg−1 of 40K, 238U and 232Th, respectively and a dose rate of 1.09 Gy·ka−1. These data allow the selection of the count time required to achieve a specified uncertainty. For example, even counting for only 1 to 2 hours gives a dose rate with a relative uncertainty ≤5%. A longer count of >5 hours brings down the uncertainty below ±3%. The sample used to illustrate these dependencies is amongst those with the lowest activity concentrations (see Fig. 4); one can expect to obtain even lower uncertainties with a shorter counting time when the samples with higher activity concentrations are measured.
. CONCLUSIONS
We have investigated the potential of full spectrum analysis (FSA) algorithm for analysing gamma spectra from a low cost, low maintenance laboratory spectrometry system based on a 3′×3′ NaI(Tl) crystal, to determine burial dose rates in trapped charge dating. Experimental results have shown that an FSA algorithm employing iterative reweighted least-squares regression is able to significantly lower the minimum detection limits (MDLs), down to 1.1, 0.09, and 0.07 Bq, respectively, for 40K, 238U, and 232Th activities (corresponding to 4.8, 0.4 and 0.3 Bq·kg−1 for a 0.23 kg sample). These MDLs are one order of magnitude lower than those based on an improved three-window analysis approach (reported earlier by Bu et al., 2018), and are comparable to those obtained from our high resolution HPGe facility (Murray et al., 2018). The MDLs for 40K, 238U, and 232Th from FSA are all almost one order of magnitude lower than those found in almost all natural sediments. We conclude that our NaI(Tl) gamma analyses based on FSA are suitable for determining the dose rate even in samples containing low activity concentrations of 40K, 238U and 232Th.
The accuracy and precision on measurement and analysis of activity concentration and dose rate have been examined in 20 natural samples. The results are also compared to those measured using an HPGe spectrometer, and we found the relative discrepancies are all within 5% on activity concentrations of 40K (RSD 2.2%), 238U (RSD 2.5%), and 232Th (RSD 2.7%), and within 4% on dose rates (RSD 1.6%). The average ratio of dose rates measured on our NaI(Tl) scintillation spectrometer with FSA to those from HPGe spectrometry is 0.993 ± 0.004 (n=20).
Further investigations of the dependence of analyses on counting time indicate that for a sample containing ∼250, 10 and 10 Bq·kg−1 of 40K, 238U and 232Th, respectively, even a 1–2 hours count time gives a result with uncertainty ≤5%. A longer counting, e.g. for 5 hours quickly brings down the uncertainty below ±3%. This demonstrates that using FSA with our NaI(Tl) spectrometer is capable of rapid and accurate determination of burial dose rate.
Given these results, we conclude that our simple scintillation spectrometry system employing FSA is a useful alternative laboratory method for accurate and precise determination of burial dose rates at a significantly lower cost than high resolution gamma spectrometry. This, combined with the relatively large (and so more representative) sample size, makes it a strong competitor to other analytical methods used in OSL dating.