. Introductions
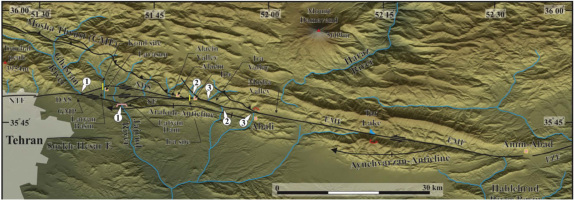
Tehran where more than 15 million people are living stands at the foothill of the central Alborz mountain, an active mountain range surrounding the southern margin of the South Caspian basin (e.g. Berberian, 1983; Jackson et al., 2002; Allen et al., 2003; Abbasi and Farbod, 2009). The border between the north part of Tehran and southern border of the Alborz mountain is marked by North Teh-ran Fault (NTF) and Mosha Fault (MF) (Fig. 1). The NTF and MF are located respectively in the northern and northeastern margins of the Tehran metropolis and repre-sent an important seismic hazard for the Iranian capital considering the historical seismicity recorded in the area (e.g. Ambraseys and Melville, 1982; Berberian and Yeats, 1999) and the active tectonics features observed along them (e.g. Berberian et al., 1985; Trifonov et al., 1996; Solaymani et al., 2003; Ritz et al., 2006).
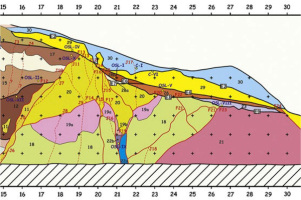
Fig. 1
Regional setting of the EMF and NTF zone showing drainage offsets across the two faults. DAS: Darabad segment of NTF, EMF: Eastern Mosha Fault, FZF: Firuzkuh Fault, GMP: Ghuchak Mountain Pass, NDS: Niknamdeh segment of NTF, NTF: North Tehran Fault zone, SF: Sabu Fault. Squares indicate towns and villages. Breakaway scarp of mass movements are shown by red barbed curves. Note the pull-apart basin in Latyan Basin depression area. Yellowbars showthe two trench sites in this study (not to scale). Arrows and numbers indicate drainage offsets of 9.3, 6.5 and 9.5 km respectively in 1, 2 and 3. Topography is from SRTM data. (Ghasemi et al., 2014).
Berberian et al., 1985 attributed the 4 B.C. Ray-Eivanekey earthquake (Ms ≈ 7.7) and the 958 A.D. Ray-Taleghan earthquake (Ms ≈ 7.7) to the activity of NTF and/or Mosha Fault. Ambraseys and Melville (1982) suggested that the earthquake in 1830 A.D. (M ≈ 7.1) was centered very close to the place where the surface expres-sions of the Eastern Mosha Fault (EMF) and NTF are linked in the Ira area (Fig. 1).
Evidence of predominant active left-lateral strike–slip faulting is found from the eastern Mosha valley to the Tehran City, all along the junction zone between the Mosha and the North Tehran faults and there is kinematic link between the EMF and NTF (Solaymani azad et al., 2011; Ghasemi et al., 2014).
Ghasemi et al. (2014) excavated and studied the Ira trench site in the easternmost part of the NTF, where it joins the MF (the Ira site) (Figs 1 and 2). The trench is located at 51°49′43″E and 35°48′23″N, at an elevation of about 2300 m . They separated thirty three units in the Ira trench, which were divided into 6 packages (I to VI), described, according to their composition, relative and absolute ages.
14C and OSL methods were used to date samples col-lected from the Ira site (Ghasemi et al., 2014). The whole package I mainly belongs to Holocene (Ghasemi et al., 2014), and provides essential constraints for the recent paleo-earthquake activity of the MF and NTF zone. Therefore, finding accurate ages for all the units of this package is very important. Package I consists of units 23, 25, 26, 27, 28, 29, 30 and 31 which the numbering of units is increasing upwards. IRA8, IRA5, IRA1, IRA4 OSL samples were collected from units 23, 26, 28 and 29, which yield OSL Central Age Model (CAM) ages of 35.0 ± 6.1, 7.3 ± 1.3, 6.4 ± 0.9 and 56 ± 6.5 ka, respectively. The ages of IRA4 and IRA8 are overestimated as compared to the stratigraphy.
The aim of this paper is to find the possible sources of age overestimation for IRA4 and IRA8 and attempts to determine ages close to true ages of these two samples. This paper will first explain the basis of OSL dating and the role of the equivalent dose (De). It will later discuss the source errors of De and explain different methods to overcome this problem. In the end it employs statistical methods to find more reliable ages for samples IRA4 and IRA8. The minimum age for IRA8 is published by Ghasemi et al. (2014) but without scientific details.
. Optically-Stimulated Luminescence (Osl) Dating of the IRA4 and IRA8
Luminescence dating is based on the measurement of two quantities, the total radiation dose the sample has been exposed to since its last exposure to daylight; this is known as the equivalent dose (De) and the rate at which it has absorbed energy from the natural environment (the dose rate). The age is obtained by dividing the palaeodose by the dose rate.
The ability to make replicate measurements of the equivalent dose (De) is central to luminescence dating. Single Aliquot Regeneration (SAR) protocol (e.g. Murray and Wintle, 2000) has enabled De estimates to be obtained from subsamples (‘aliquots’) composed of a few hundreds of grains or a few tens, and even from single grains (e.g. Roberts et al., 1998, 1999; Jacobs et al., 2003; Olley et al., 2004).
The process of calculating De using the SAR procedure is described in Table 1. It involves measurement of the natural luminescence signal (LN) arising from irradiation in nature, assessing the sensitivity of the aliquot by measuring the luminescence signal (TN) generated by a test dose (DT), and then undertaking a number of cycles each of which involves irradiation (D1, D2, D3, etc.) to regenerate the luminescence signal (L1, L2, L3 etc.), followed by a test of the sensitivity (T1, T2, T3 etc.) using the test dose. The value of De is then found by comparing the ratio RN (= LN/TN) with an appropriate mathematical equation which fits the resulting ratios R1, R2, R3 etc. (obtained from L1/T1, L2/T2, L3/T3 etc.) to determine the laboratory dose that generates a signal equivalent to that obtained from the natural (Duller, 2007). Using the SAR protocol, each aliquot provides an independent estimate of De, and by taking measurements on many separate aliquots the distribution of De within a sample can be assessed (Duller, 2008).
Table 1
Generalized single aliquot regenerated sequence and outline of the steps involved in the SAR method. *Observed Lx and Tx are derived from the initial IRSL signal (2 s) minus a background estimated from the last part of the stimulation curve. Corrected natural signal N = L0/T0; Corrected regenerated signal Rx = Lx/Tx (x = 1–5). Note that in step 2, the sample has been heated to the pre-heat temperature using TL and held at that temperature for 10 s.
| Step | Treatment 1 | *Ob |
|---|---|---|
| 1 | Give dose | – |
| 2 | Pre-heat (TL 200–300°C) | – |
| 3 | Stimulation (at 120°C) | LX |
| 4 | Give test dose | – |
| 5 | Cut-heat (TL 120–260°C) | – |
| 6 | Stimulation (at 125°C) | TX |
| 7 | Return to 1 | – |
However, to determine a reliable De for a sample, the amount of variation between De estimates for different grains in an aliquot, or different aliquots that have absorbed the same radiation dose should be investigated.
An understanding of all sources of scatter contributing to such estimates should be well understood or quantified (Galbraith et al., 2005; Stone and Bailey, 2012).
The sources of uncertainty and scatter of De estimate
The commonly observed scatter in De distributions of sedimentary samples can be attributed to different sources, referred to by Thomsen et al. (2005) as ‘extrinsic’ and ‘intrinsic’ sources of uncertainty. The former sources include: post depositional mixing of grains from adjacent sedimentary layers (e.g. Roberts et al., 1998 and 1999; Bateman et al., 2003, 2007a; Feathers et al., 2006; Jacobs et al., 2006; David et al., 2007) and dosing, poor or heterogeneous bleaching of grains prior to burial (e.g. Olley et al., 2004; Bøtter-Jensen et al., 2000; Duller and Murray, 2000; Duller et al., 2000; Murray and Olley, 2002; Olley et al., 1999, 2004), and dosing, particularly at the micro-scale in the beta-radiation field such as beta-dose heterogeneity in the natural burial environment (e.g. Olley et al., 1997; Murray and Roberts, 1997; Nathan et al., 2003; Mayya et al., 2006; Jacobs et al., 2008a, 2008b).
‘Intrinsic’ sources of inconsistency include differences in the OSL signals response from different grains to identical treatments (e.g., Bailey, 2002, 2004) or differing grain-to-grain responses to fixed SAR conditions (e.g. Jacobs et al., 2003); statistical uncertainty due to photon counting and instrument uncertainties and luminescence measurements and then their combination to determine De (e.g. Thomsen et al., 2005; Duller, 2007), such as thermal transfer and photo-transferred recuperation (i.e. transfer of charge from thermally shallow but optically insensitive traps to the deeper trap responsible for the OSL signal, as a result of laboratory heating, optical stimulation, or a combination of the two) (e.g. Aitken and Smith, 1988; Stokes, 1992; Banerjee, 2000). Internal variability leads to the observation of different ‘grain behavioural types’, seen in luminescence properties such as brightness and dose response characteristics (e.g. Murray and Roberts, 1997; Roberts et al., 1999; Yoshida et al., 2000; Jacobs et al., 2003, 2006, 2008b; Stone and Bailey, 2012).
However, an essential assumption of the method is that the luminescence signal from a grain can be reset, or zeroed, by exposure to sufficient daylight. This is a process commonly termed ‘bleaching’ and occurs in many processes of erosion, transportation or deposition, particularly those that occur sub-aerially. Where all the grains in the sample were exposed to sunlight for sufficient time at deposition to remove any trapped charge, then the sample is fully bleached and all grains would have a De of zero at deposition, and after some period of burial all the aliquots would give the same value of De (e.g., aeolian sediments). Where the luminescence signal from some of the grains were not zeroed, grains would have different De values at the time of deposition; this is termed incomplete or partially bleaching (e.g., alluvial and colluvial sediments) (Duller, 2007).
Sediment mixing by post depositional processes is a dominant source of De variability across a range of sedimentary environments even in quartz-dominated, well-bleached, aeolian, dryland sediments (e.g. Arnold and Roberts, 2009 and references therein). Recognition of sediment mixing in the field is often difficult because the absence of depositional bedding structure is not neces-sarily indicative of sediment mixing, whilst the presence of sedimentary structure does not necessarily prevent post-depositional disturbance (Bateman et al., 2007a).
The appearance of De distributions can be affected by the kind of post-depositional processes. The dominant younger (or older) grains intrusion increases positive (negative) skewness. It can increase symmetrically the overall spread of De values, or create discrete dose populations (including zero-age grains) and multi-modal De distributions. Arnold and Roberts (2009) reported some of the important issues associated with the analysis of mixed De distributions, using simulated De data sets produced with a simple stochastic model.
However, partial bleaching and post-depositional mixing of young/old samples cannot be overcome through optimisation of experimental apparatus and measurement conditions and needs to be addressed via careful statistical analysis of De distributions and use of appropriate statistical age models.
Several statistical age models have been suggested to obtain estimates from the burial dose associated with only the most fully bleached (and undisturbed) grains in each sample (e.g., Olley et al., 2004; Bailey and Arnold, 2006; Arnold and Roberts, 2009); or of the post-depositionally mixed sediments (e.g. Roberts et al., 2000; Spencer et al., 2003; Sivia et al., 2004).
The most statistically suitable of these are the mini-mum age model (MAM) of Galbraith and Laslett (1993) for OSL dating of samples that not all the grains have been fully bleached.
The finite mixture model (FMM) of Galbraith and Green (1990) has been used in a number of recent OSL studies of mixed sediments (e.g. Roberts et al., 2000, 2001; Jacobs et al., 2006, 2008b; David et al., 2007; Bateman et al., 2007b).
In this study Mark Bateman spreadsheet was used to calculate the FMM and the program for MAM calculation was provided by Sebastien Huot.
OSL methodology
Quartz was extracted and cleaned under low-intensity red light at the Sheffield Centre for International Dryland research luminescence laboratory. Carbonates and organ-ics were removed with HCL and H2O2. A 45 minutes HF treatment was followed after heavy minerals separation (S.G. 2.7 gcm-3). IR stimulation revealed no feldspar contamination. Standard medium single-aliquot dating of the 90–250 μm quartz fractions of samples IRA1, IRA4, IRA5 and IRA8, was performed using standard protocols as outlined in Fattahi et al. (2006).
To test if there were problems from the thermal trans-fer of charge into the OSL trap as a result of preheating, natural aliquots of sample IRA4 were stimulated at room temperature without any prior preheating and OSL was measured for 100 s. After more than 4 h delay the OSL was measured again. No significant OSL signal was ob-served for the second measurement. Then, SAR was applied to measure the De at different preheat tempera-tures (expected to be zero in ideal scenario). All subsequently measured apparent values of De were less than 0.4 Gy for preheat temperatures from 170°C to 300°C. This is small compared with typical natural De and suggests that the samples do not suffer from significant thermal transfer.
Dose recovery preheat tests (as per Murray and Wintle, 2000, 2003) were carried out and showed that overall effects of sensitivity changes had been properly corrected for and known laboratory doses were recovered by the SAR protocol. The mean ratios of measured to given doses for IRSL were statistically consistent with unity.
Some aliquots were rejected as they were dim or the recycling values were not within 10% of unity. Some aliquots produced a reasonable OSL signal of which some passed the SAR criteria. These aliquots were chosen for De determination. The CAM provided average ages close to large aliquots for all four samples. The ages of IRA4 and IRA8 were overestimated as compared to the stratigraphy.
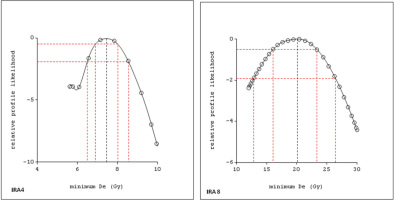
The single-aliquot De distributions and the relative profile likelihood graphs are shown in Figs. 3 and 4. A common feature of the De values of these samples is the widespread distribution of equivalent doses. The spread of single aliquot De values are because of ‘experimental’ and ‘natural’ variations. Experimental errors are reducible but natural variation is inherent. When more than 5% of De values lie outside ±2σ of the central value, the dose distribution is termed over dispersed. Over-dispersion (OD) is a quantitative estimate of the amount of spread in the De data set after allowance has been made for measurement uncertainties (Galbraith et al., 1999; Roberts et al., 2000; Galbraith et al., 2005; Galbraith and Roberts, 2012). Many studies have reported up to 20% over-dispersion among De estimates for single aliquots and individual grains that are known or thought to have been well bleached (e.g., Roberts et al., 2000; Olley et al., 2004; Thomsen et al., 2005; Jacobs et al., 2006; Galbraith and Roberts, 2012).
Fig. 3
The De value of IRA samples, representative radial plots of ‘mixed and scattered’ single aliquot De distributions. The grey bands show values of 2 standard deviations from the De CAM estimates (Galbraith et al., 1999) for IRA1 and IRA5. The solid yellow lines show the MAM De, and interpreted as representing almost totally bleached grains, which were used for sample De and age determination. The soild gray lines in IRA4 and IRA8 show FMM De. Over dispersion for IRA1, IRA4, IRA5 and IRA8 are 30, 92, 25 and 57, respectively
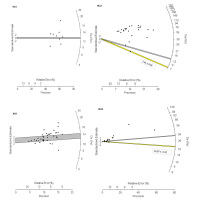
The De of IRA1 and IRA5 is not as widely spread as IRA4 and IRA8. Their OD (30% and 25% for IRA1 and IRA5, respectively) is low compared to IRA4 (92%) and IRA8 (57%).
But what are the sources of the wide spread De of medium aliquot measured samples? A medium aliquot is still an average of many grains and may hide the wide spread of De’s of single grains inside medium aliquots. An OD value of ~6% was obtained for the dose recovery data sets for sample IRA4, so high over-dispersion cannot be due to inherent differences. Therefore, other sources, such as grain-to-grain variations of bleaching and bioturbation may contribute to De scatter for IRA4 and IRA8 samples, with high over-dispersion values (92% and 57%).
Model selection for De determination
Various statistical methods have been developed to isolate grains which represent a true burial dose. For well bleached samples one of the mean calculation methods such as central age model is commonly used. If there are samples that contain a mixture of grains with different bleaching histories, the minimum age model is suitable to determine the minimum age provided by fully bleached grains. The finite mixture model enables one to estimate the number of dose components within a dose distribution and the corresponding De for each component. The lowest component is the youngest cluster of Des.
In order to consider among different statistical approaches which age model is more suitable for our sam-ples, the age model decision process by Arnold et al. (2007) and Bateman et al. (2007a) was used. Specific De distribution characteristics (e.g., over-dispersion, skew-ness) were taken to identify the appropriate statistical approach.
These age model decision processes suggested the use of CAM for IRA1 and IRA5, and MAM and FMM for IRA4 and IRA8 samples.
The suggestion of age models is consistent with reality. IRA4 and IRA8 samples most likely include grains from different sources and time scales. They are from the environment that the sediments are fluvial, or colluvial. Therefore, grains are likely to be incompletely bleached. MAM is a suitable model to be employed to provide the ages of these samples.
FMM can separate different clusters of Des and suggest an average for each cluster. IRA4 and IRA8 are sampled at the bottom of the units 29 and 23, respective-ly. Therefore, it is probable that these samples include post-depositional grain through bioturbation from the layer below. For example the age of underlying unit (unit 17) of sample IRA4 was 85.4 ± 12.1ka, and transfor-mation of grains from this unit to sample IRA4 obviously increase the average age of IRA4. This can be the reason that IRA4 has overestimated the age of unit 29. In this circumstance the age of youngest cluster of FMM can provide the true age of aimed unit.
Therefore, on the basis of the De scatter, age model decision process and stratigraphy, it has been concluded that, MAM (13.1 ± 4.3 and 3.5 ± 0.3 ka) and the first component of FMM (21.5 ± 2.2 and 6.1 ± 0.6 ka) may give a better indication of the deposition age, rather than CAM (35 ± 6.1 and 58.1 ± 6.5ka) for IRA8 and IRA4 samples, respectively. If we combine the age provided by first component of FMM and the age provided by MAM OSL, it will give us 8.8–23.7 and 3.2–6.7 ka for units 23 and 29, respectively. These ages are more consistent with stratigraphy.
. Discussion and Conclusion
Values used to calculate Annual dose rate and the Des used to calculate luminescence ages are shown in Table 2 and Table 3, respectively. The MAM age of sample IRA4 (3.5 ± 0.3 ka) is more compatible with the overall stratigraphic chronology of the exposed units, and is much closer to the radiocarbon age of sample Ira.2008/C-IV (1105 ± 30 yr BP) collected from the underlying unit 27 (Ghassemi et al., 2014) than CAM age of sample IRA4 (58.0 ± 6.5 ka). However, the radiocarbon age of sample Ira.2008/C-IV (1105 ± 30 yr BP) is still discrep-ant with this recent MAM age. This apparent discrepancy means that the age of one of these samples or both sam-ples do not represent the age of their units.
Table 2
Values used to calculate Annual dose rate from IRA trench. Uncertainties are based on the propagation, in quadrature, of errors associated with individual errors for all measured quantities.
Table 3
Des used to calculate luminescence ages employing three different statistical methods, Central age model (CAM), Finite mixture modelling (FMM) and Minimum age model (MAM).
| Sample ID | De (Gy) | Age (ka) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAM | ± | FMM | ± | MAM | ± | CAM | ± | FMM | ± | MAM | ± | |
| Ira.I | 11.4 | 1.3 | 6.4 | 0.9 | ||||||||
| Ira.IV | 123.9 | 11.0 | 13.0 | 0.9 | 7.5 | 0.6 | 58.0 | 6.5 | 6.1 | 0.6 | 3.5 | 0.3 |
| Ira.V | 13.3 | 2.0 | 7.3 | 1.3 | ||||||||
| Ira.VIII | 53.3 | 7.9 | 32.7 | 0.9 | 20.0 | 6.3 | 35.0 | 6.1 | 21.5 | 2.2 | 13.1 | 4.3 |
If the radiocarbon age of sample Ira.2008/C-IV (1105 ± 30 yr BP) does not represent the age of unit 27, it means that this sample may have been emplaced much later than the true burial age of unit 27. This support the idea that unit 27 could be older than the three colluvial wedges (units 23, 26, and 28) and these three colluvial wedges (units 23, 26, and 28) have been formed by three paleoearthquakes applying reverse component on fault F13, and mostly these colluvial wedges are reworked units that have been derived from unit 27. This could also be a plausible explanation of the anomalous young radio-carbon age of sample Ira.2008/C-III (950 ± 30 yr BP) compared to the OSL age of overlying unit 25 (sample Ira.2008/OSL-VI: 8.7 ± 1.6 ka, see Tables 1 and 2 of Ghassemi et al., 2014). However, if Ira.2008/C-IV (1105 ± 30 yr BP) underestimate the age of unit 27, combining the stratigraphic order between units 27 and 29 with the MAM age of OSL sample IRA4 (3.5 ± 0.4 ka) does not permit Ghassemi et al. (2014) to use the radiocarbon age of sample Ira.2008/C-IV (1105 ± 30 yr BP) to identify a possible seismic event at the base of unit 27, to be associated with the 958 AD Ray-Taleghan event (M ≈ 7.7).
If the MAM age of sample IRA4 (3.5 ± 0.4 ka) has overestimated the true burial age of unit 29, it has positive effect on the interpretation of Ghassemi et al. (2014) to associate trench seismic events to some historical events (e.g., unit 27, to be associated with the 958 AD Ray-Taleghan). Particularly, it may confirms Ghassemi et al. (2014) interpretation that units 23, 26, 29, and 30 have been cut by faults F24 to F28 in the northern end of the Ira trench, which interpreted as likely of seismic origin associated with the 1830 AD earthquake of Damavand–Shemiranat (M ≈ 7.1) earthquake, the meizoseismal area of which was centered on the junction between the Mosha and NTF, very close to the Ira site (Fig. 1).
The De overestimation of samples IRA4 and IRA8 can be due to many parameters, including post-depositional mixing and partial bleaching. Both samples are collected from the bottom of their units and the positions of samples are very close to the bottom unit. As a result it is likely that overestimation is due to the inclusion of grains with much higher De either due to upward movement within the profile of older grains (through bioturbation). The signature of post-depositional mixing in principle can be determined at the single-grain scale of analysis, as individual grains that have intruded from older units may be identified as discrete components in a De distribution. We expect by employing single aliquot measurements, the variation in De decrease, but still the minimum cluster of De (first component of FMM) is closer to true age in compare to average De (CAM) for samples that may suffer from partial bleaching or post-depositional mixing.
In order to date partially bleached sediment, it is im-portant to estimate the amount of scatter caused by grain-to-grain variability in the natural dose rate. Measurements of such scatter are performed at the single-grain level; by contrast, most OSL dating is performed on multi-grain subsamples, for which grain-to-grain scatter is reduced through averaging. Therefore, the single aliquot MAM age of sample IRA4 (3.5 ± 0.4 ka) may has overestimated the true burial age of unit 29.
We tried the conventional method of single grain analysis but due to dim signal, it was not possible to do reliable single grain measurement for our samples. We believe there is no harm to apply MAM and FMM for single aliquot analysis of scattered De. Because only in the absence of De scatter relating to partial bleaching or sediment mixing, CAM provides a representative esti-mate of the average sample burial dose (Galbraith et al., 1999). But in the cases that we are not sure that partial bleaching or sediment mixing is absent, or there are evi-dences that they may exist, MAM and FMM can be ap-plied for single aliquot to provide a closer age to true age.
The 4 BC Ray-Eivanekey earthquake (Ms ≈ 7.7) is suggested to be related to Kahrizak, Garmsar or Parchin active faults. However, it might have triggered either NTF or MF in the Ira site and has produced one of the colluvial wedges or other past earthquake evidence. However, the presented age controls do not permit one to explicitly assign the 4 BC earthquake to one of the recog-nized past earthquakes in the trench site.
Future direction
At the multi-grain scale of analysis, however, any heterogeneity in De that individual grains have, may still be masked, as individual De estimates are obtained from aliquots containing several tens, hundreds of grains. The presence of intrusive grains may therefore become ‘covered’ in the final De estimates of individual aliquots that contain a variety of both younger/older intrusive grains and in situ grains. By averaging, as the number of grains that are measured (i.e. the number of grains on each aliquot) increases, the variation in De will decrease (Olley et al., 1999; Wallinga, 2002).
Therefore, due to dim signals of the limited measured aliquots, the best way to find the accurate age for these units is to collect more and bigger samples and try to find shine grains and date them using single grains or very small aliquots.