1. Introduction

Understanding centennial to millennial scale morpho-dynamics of fluvial systems is considered important for sustainable management and restoration of rivers (Brierley and Fryirs, 2005; David et al., 2016; Delile et al., 2016). To place local observations within the broader context of the environmental and human history, it is necessary to determine the timing of fluvial dynamics. This is commonly done by analysing aerial photographs, documents, and old maps (Bristow, 1987; Hohensinner et al., 2004; Arnaud et al., 2015; David et al., 2016), but these are not pervasively available on all temporal and spatial scales. Hence, it is often necessary to date fluvial deposits and use this information for the reconstruction of past river dynamics.

The most common method in this context is radiocar-bon dating, but it suffers from two major problems. First, most organic material in fluvial environments is reworked and radiocarbon dates may hence overestimate the true age of fluvial deposition (e.g., Howard et al., 2009; Delile et al., 2016). While this problem can be reduced by sampling aquatic plant remains, identification of such material is not always straightforward. Second, there are several plateaus in the radiocarbon calibration curve of the last few centuries that will produce very large uncertainties. For example, a radiocarbon age of 120 ± 2 ¹⁴C yr corre-sponds to a calendric age of 149 ± 79 cal. BP (AD 1722 – 1880, Reimer et al., 2009), which may be too imprecise to sufficiently address certain scientific questions. Alternatively, ²¹⁰Pb and ¹³⁷Cs geochronology can be used but only in low-energy depositional environments and for very young deposits (e.g., Jweda and Baskaran, 2011; Mabit et al., 2014).

Optically Stimulated Luminescence (OSL) dating utilises a light-sensitive latent signal in quartz and feldspar grains induced by ionising radiation, mainly originating from radioactive decay of K, Th and U and their daughter isotopes (cf. Preusser et al., 2008). During sediment transport the signal is depleted (bleached) by daylight and starts to accumulate after burial, when the grains are sealed from light exposure. Madsen and Murray (2009) and Pietsch (2009) summarise the specific methodological aspects related to the dating of young deposits (defined here as ages < 1000 years), and show that OSL can produce reliable ages as young as a few years. For example, Madsen et al. (2005) dated sand-sized quartz extracted from estuarine sediments of the Danish Wadden Sea and found excellent agreement between OSL and ²¹⁰Pb dating in the younger part of their core (< 60 years). However, there are several problems associated with OSL dating of young sediments, in particular with the determination of Equivalent Dose (D_e). The latter represents the radiation dose absorbed by the grains since the event to be dated, as reflected by the strength of the natural OSL signal. In the laboratory, D_e is determined by comparing natural OSL with OSL signals induced through laboratory radiation. OSL ages are calculated as ratio of De and dose rate, i.e. the amount energy emitted by radioactive elements through ionising radiation per year, and reflect the time of sediment deposition, if the OSL signal was completely bleached prior to deposition.

For young sediments, little signal will have accumulated as grains have been exposed to ionising radiation for only a short periods of time, which can be problematic with regard to the signal-to-noise ratio. In particular, this applies to quartz and appears to be related to a lack of dosing and exposure cycles that would cause a sensitisation of the electron traps in quartz (Pietsch et al., 2008; Sawakuchi et al., 2011). Thus, while quartz is clearly the preferred mineral for the dating of young sediments, there are several settings where its application is not feasible because in some regions quartz does not exhibit any detectable OSL signal at all, corresponding to immature dosimetric properties of the quartz (e.g. Preusser et al.,2006; Jeong and Choi, 2012). In such cases, Infrared Stimulated Luminescence (IRSL) from feldspar might be the only option, but this signal can be unstable with time. This anomalous fading of the feldspar signal will cause underestimation of De, hence of the sedimentation age (Wintle, 1973; Spooner 1994). However, it appears that the degree of fading depends on mineral genesis, with plutonic feldspars fading less than those of volcanic origin (Visocekas and Guerin, 2006). It has been presumed that anomalous fading results from tunnelling of charge that follows strict physical laws, i.e. the signal decays logarithmically (Visocekas, 1985). Following these assumptions, Huntely and Lamothe (2001) developed a procedure to correct for fading. First, storage experiments are carried out to monitor the loss of signal with time. The results of such experiments are expressed by g-values, where g is the signal loss in percent per decade, a decade being a factor of 10 in time since irradiation (Huntely and Lamothe, 2001). The g-value is then used to correct for the signal loss since burial. However, several studies report that the signal loss observed in experiments does not represent the fading of the signal over geological periods (e.g. Wallinga et al., 2007; Lowick et al., 2012; Preusser et al., 2014). Guérin and Visocekas (2015) discuss that anomalous fading likely results from at least two different mechanisms, one of which is temperature dependent, and the tunneling - a pure quantum mechanical athermal process. The implication is that the fading correction proposed by Huntely and Lamothe (2001) might not be accurate as temperature under laboratory conditions might differ from that in nature. Hence, fading correction may tend to either over- or underestimate the true age of a sample, depending on the nature and climate history of a sampling context.

Thermal transfer and recuperation, both representing a transfer of electrons from thermally shallow, light-insensitive traps to deeper, light-sensitive traps, occur when grains are preheated during the measurement procedure to remove unstable components of the OSL signal that are induced by laboratory irradiation (Aitken and Smith, 1988;Rhodes and Bailey, 1997). Following Wintle and Murray (2006), ‘thermal transfer’ is used here only for the transfer of charge during the first preheating of the sample, i.e. it effects only the natural signal. As thermally transferred OSL is not present in the build-up of the signal in nature, i.e. it is a laboratory artefact, this phenomenon will lead to overestimation of the real OSL deposition age. The effect of thermal transfer can be monitored by removing the light sensitive signal by light exposure and measuring the signal induced by preheat (thermal transfer test). The term ‘recuperation’ describes charge transfer during preheat following laboratory irra-diation. It is monitored by including a zero dose step in the measurement procedure (Murray and Wintle, 2000).

Overestimation of ages will also occur when the OSL signal was incompletely reset at the time of deposition, as the signal acquired since the event to be dated will add on top of the residual signal. However, as each grain has its own daylight exposure history, the residual level in grains will differ in the presence of incomplete resetting; grains will be differentially bleached (Duller, 1991). Hence, measuring several dozen to a few hundred individual grains and investigating the spread will provide information on the degree of bleaching at the time of deposition (Li, 1994; Murray et al., 1995; Olley et al., 1998). Differential bleaching will be indicated by a positive skew and a broad spread of the data. The spread of data is expressed by the overdispersion value that describes the variability of the data beyond the one expected from measurement uncertainties (cf. Galbraith and Roberst, 2012). In this context it has to be noted that usually the spread of single grain values is not just the result of incomplete bleaching, but in particular dosimetric effects (Lepper et al., 2000; Vandenberghe et al., 2003). As a consequence, special statistic approaches such as the Minimum Age Model (MAM) of Galbraith et al. (1999) have been developed that consider additional sources of variability when extracting a mean De value that represents the well bleached population of grains. Application of the MAM requires one input value (σ_b) that represents the expected overdispersion from all other effects except partial bleaching. As this value is not known, it can only be estimated by comparison with similar sediments that are not affected by incomplete bleaching.

deally, luminescence dating would be carried out using single grain measurements as this will provide the full information about individual grain history. However, as this approach is quite laborious, De measurements are often made on aliquots consisting of several dozen grains. Here, it has to be considered that usually only few percent of the grains (in particular for quartz) exhibit OSL signals (e.g. Duller, 2004). Hence, using aliquots with not more than 100 grains will almost mimic single grain measurements. However, in particular for feldspar separates a much larger number of grains may exhibit luminescence signals. In such cases multi-grain approaches can cause averaging of the signal originating from individual grains and mask incomplete bleaching at least to some extent (Wallinga, 2002).

Several previous studies have shown that young aeolian and coastal sediments are suitable for the dating of young deposits using quartz, as partial bleaching has little effect. There are quite a few studies that have used quartz to date young fluvial deposits (e.g. Murray et al., 1995; Olley et al., 2004), and it has been shown that incomplete bleaching needs to be considered in this context (Pietsch, 2009). For example, sediments filling up a harbour basin along the River Danube east of Vienna, which wooden structure has been dendrochronologically dated to the middle of the 16^th century, revealed three consistent OSL ages using MAM of around 500 years (Fiebig et al.,2009). However, it is also important to note that, with a few exceptions (e.g. Porat et al., 2009), almost all previous studies on young fluvial sediments used quartz as it is considered of being less affected by incomplete bleaching than feldspar.

Presented here is a case study testing the potential of feldspar IRSL to date very young fluvial deposits from a moderate/low-energy braiding/anastomosing river system from a temperate environmental setting. We took five samples from a sediment sequence that deposited in a former main channel of the River Rhine near Strasbourg, and which has been disconnected upstream by engineering works in the early part of the 19^th century, as documented by a large set of historical maps. A series of performance tests to characterise the signal, and a comparison of multi-grain (small aliquot) and single grain IRSL dating was carried out. Besides the importance for future projects on river systems in Western Europe, the results presented are considered relevant for similar studies in others parts of the planet, where quartz shows nonsuitable OSL signals.

2. Regional Context

The Upper Rhine is one of the most altered fluvial systems in Europe (Fig. 1a), with important engineering works along about 200 km and 90% of its floodplain converted into arable and industrial areas (Cioc, 2009; Herget et al., 2005). While the Upper Rhine river management had originally focused mainly on navigation, hydropower generation and flood control, several restoration projects over the past three decades have aimed at improving biodiversity and ecological functioning, groundwater protection, and development of recreational areas (Schmitt et al., 2009). The study area, the ‘Rohrschollen’ artificial island, is located 8 km SE of the city of Strasbourg and bounded by the Rhine canal (West) and the old Rhine (East) (Fig. 1b). It results from correction and canalization works that have been implemented in this area from the beginning of the 19^th century until AD 1970 (Fig. 1b). A restoration project aims at reconnecting the ‘Bauerngrundwasser’ to the River Rhine through a floodgate and a new channel (Fig. 1c). The studied excavation site is located on the right bank of this channel. Sedimentological investigations and historical research are currently carried out to improve the under-standing of the temporal trajectory of the area, better explain its modern morpho-sedimentary characteristics, and assess the potential benefits of the restoration in the future.

Fig. 1

a.) Overview of the River Rhine catchment with the location of Strasbourg. b.) Comparison of the Upper Rhine system before and after river engineering works in the 19^th and 20^th century. c.) Historic development of the study area from AD 1778 until 2010.

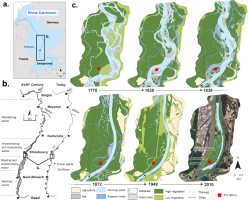
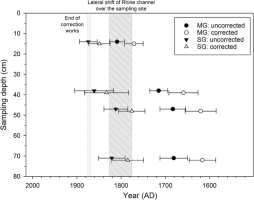
The study of old maps reveals that the upstream reach of the main watercourse of the island (the ‘Bauerngrundwasser’) was the thalweg of the River Rhine in AD 1828 (Fig. 1c). The excavation pit sampled for this study was located on a median bar of the Rhine braiding system at this date. During the correction works between AD 1828 and 1872, the River Rhine was forced artificially into an easterly direction. This caused a drastic decrease of flood energy and induced an important channel narrowing and disappearance of bars by vegetation overgrowth, as is shown on the maps of AD 1838, 1872 and 1949 (Fig. 1c). Prior to the correction works, between AD 1778 and 1828, the Rhine thalweg naturally and progressively moved from east to west, and this movement would have eroded any older fine sediments at the excavation site. Assuming that the main channel of the River Rhine passed this position sometime between AD 1790 and 1810 gives the maximum age of the sediments investigated here (225–205 years).

3. Methods

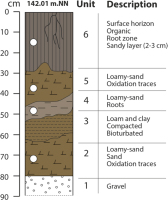
Samples have been taken by hammering opaque tubes into the freshly cleaned surface of the exposure in a small trench (Fig. 2). Sediment from the inner part of the tubes was retrieved in the laboratory under subdued red-light conditions. The fraction 150–200 μm was extracted by wet sieving, and for one of the originally five samples (RO1–3) too little material was gained to allow for further preparation. The sample material was subsequently treated by 15% HCl, 30% H₂O₂ and Na-oxalate (in combination with ultrasonic treatment) to remove carbonates and organic matter as well as to disperse clay particles. Initial tests revealed the absence of OSL signals in quartz and we hence focused on K-feldspar that was separated using heavy liquid (sodium polytungstate, δ = 2.58 g cm⁻³). Dried grains were either fixed on stainless steel discs by a 2 mm spot of silicon oil (multi-grain measurements) or transferred to special Riso single grain discs.

Fig. 2

Schematic sketch of the sampled exposure.

Multi-grain measurements were performed on a Lexsyg smart device (Richter et al., 2015), whereas single grains were analysed on a Ris⊘ DA-20 reader with a dual laser single grain attachment (BØtter-Jensen et al., 2003). For both devices similar detection filter sets have been used (Lexsyg smart: Schott BG39, AHF BrightLine HC 414/46; RisØ DA-20: Schott BG39, L.O.T.-Oriel D410/30 nm) and stimulation was done at 50°C. Performance tests (thermal transfer, dose recovery, and fading) were carried out for multi-grains and single grains (except thermal transfer for the latter). To minimise the effect of thermal transfer of charge, preheat temperatures of 150°C, 170°C and 190°C were tested, with a duration of 10 s each. Prior to the tests, multi-grain aliquots were exposed for 300 s to the light of the in-build blue LEDs (458 nm peak emission, 100 mW cm⁻²) followed by IR stimulation (850 nm peak emission, 180 mW cm⁻²) to confirm the absence of IRSL signals. For single grains, the signal was removed during a 24 h exposure to a UV lamp.

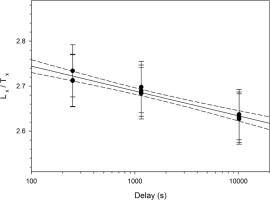
Storage tests to monitor IRSL signal decay due to fading have been carried out at room temperature (c. 20°C) on multi-grain aliquots and single grains that were previously used in the dose recovery test and applying a dose of 39 Gy. This much larger dose than in the natural was chosen to improve reproducibility, as the single grains signal are not very bright. Immediate measurements of L_x/T_x (ca. 250 s between half-time irradiation and beginning of stimulation) and two delayed measurements (1150 s, 10,150 s) were carried out and repeated three times. Preheat was applied immediately after the irradiation, i.e. before the storage. From this data, g-values have been calculated following Huntley and Lamothe (2001).

Measurement of D_e was done using the Single Aliquot Regenerative Dose (SAR) protocol (Murray and Wintle, 2000) modified for feldspar following Preusser (2003) and Blair et al. (2005). For multi-grains this included preheating for 10 s prior to all IRSL measurements (see below for comment on temperature), followed by 100 s IR LED stimulation (850 nm peak emission, 180 mW cm⁻²). The IRSL signal 0-10 s was used for integration by subtracting the signal 10-30 s as background. IRSL of single grains was stimulated for 5 s using a 140 mW 830 nm laser (90% laser power) with a RG-780 filter to attenuate the second harmonic frequency (415 nm). Single grain signals were integrated over the initial 0.2 s, and the background signal was averaged over the last 0.5 s. About 50 multi-grain discs have been measured for samples RO1-2, RO1-5 and RO1-6, but for RO1-4 the amount of material available allowed only for 24 replicate measurements. For single grains, seven discs each containing 100 grains per sample have been prepared. We abstain from applying post-IR IRSL methodology as residual doses of up to several Gy have been observed in bleaching experiments and in modern analogues (Trauerstein et al., 2014; Smedley et al., 2015). According to Reimann et al. (2012), residual dose gives rise to an offset of 0.6 Gy in their coastal samples, which is a about twice the value expected for the samples under consideration here. Furthermore, partial bleaching will be likely more problematic in fluvial environments.

Measurement results have been analysed using Analyst 4.31.9 (Duller, 2016) and were further handled in home-made Excel sheets. All multi-grain discs passed the usual rejection criteria (recycling ratios within 10% of unity, 10% test dose error, test dose signal min. three times above background; cf. Wintle and Murray, 2006). Grains with a signal >3 sigma above background, a test dose error <15% and a recycling ratio between 0.90 and 1.10 (considering uncertainties) were selected for D_e determination. Further grains were rejected, if the recuperation expressed in percentage of the regenerative signal was >10%, or if the natural signal was above dose response saturation level. Of all measured single grains between 7.3 and 11.2% passed all applied rejection criteria and were used for D_e calculation. For all samples, mean D_e was calculated using the Central Age Model (CAM) and the MAM-3 (Galbraith et al., 1999), as the observed overdispersion and shape of the distributions strongly imply the presence of partial bleaching (see below). MAM-3 calculations were carried out using the R-Luminescence package (Kreutzer et al., 2012; Fuchs et al., 2015), and the effect of varying the σ_b value is discussed below.

The concentration of dose rate relevant elements (K, Th, U) was measured using high-resolution gamma spectrometry, similar to the procedures described by Preusser and Kasper (2001). Using the approach of Preusser and Degering (2007), we observed no evidence for radioactive disequilibrium in the Uranium decay chain. Age calculations were carried out using ADELE 2015 software using present day geographic position and burial depth, assuming an a-value of 0.07 ± 0.02, and estimating sediment moisture based on sediment composition and hydrological context (allowing for large uncertainties). An internal K-content of 12.5 ± 1.0% was used based on values reported by Gaar et al. (2014) for northern Switzerland. Dose rate calculation was done using a three-layer model to account for inhomogeneity between the different sedimentary units (Table 1). The differences to using a classical one-layer model are, however, minimal (max. 2% for sample RO1-6).

4. Results and Discussion

IRSL properties

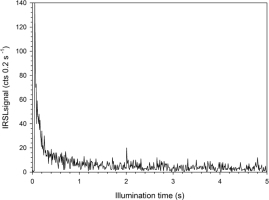
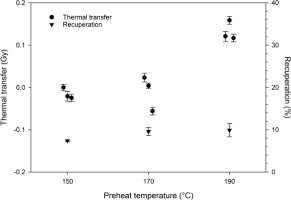
The feldspar shows a moderate response to IR stimulation in the multi-grain approach with close to linear growth of dose response curves (Fig. 3), whereas the single grain IRSL response is quite low and a little noisy (Fig. 4). Thermal transfer when applying the two lower preheat temperatures is close to zero but increases significantly when using a preheat of 190°C. Recuperation is 7.40 ± 0.18% (of the applied ‘recovery’ dose signal) when preheating at 150°C but > 9% for the two higher preheat temperatures (Fig. 5). Hence, we used preheating at 150°C for 10 s in all following experiments and for D_emeasurements, for both multi- and single grains. For the latter, recuperation is significantly higher but this is explained by the much lower signal-to-noise ratio.

Fig. 3

Example of IRSL decay for a multi-grain disc and a dose response curve of sample RO1-4 (inset).

Fig. 4

Representative single grain IRSL decay of sample RO1-4.

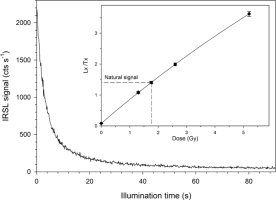
Fig. 5

Results of thermal transfer tests experiments reveal a slight increase of D_e with increasing preheat temperature. Same applies for recuperation as monitored in the dose recovery experiments.

The multi-grain dose recovery experiment reveals an excellent reproducibility of the applied dose with a recovery ratio of 1.03 and a relative standard deviation of 2.3%, which corresponds to the average uncertainties of individual measurements (Fig. 6). The overdispersion in the dose recovery experiment was 2.1 ± 0.1% and is reduced to zero when assuming an instrumental uncertainty of 1.4%. This instrumental uncertainty was used when analysing multi-grain D_e measurements. The single grain dose recovery experiment reveals a dose recovery ratio of 1.07 ± 0.01 with an overdispersion of 7%, if no instrument error is assumed (Fig. 6). Overdisperison drops to 4.9% if an instrumental error of 2.5% is used (Trauerstein et al. 2012).

Fig. 6

Results of the dose recovery tests for both multi-grain aliquots and single grains.

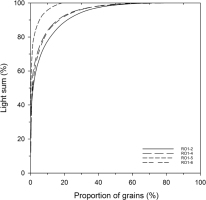
The light-sum plots (Fig. 7) show that in three of the samples (RO1-2, 4, 6) about 10% of all grains are responsible for 80% of the light emitted. The remaining 20% of the signal origin from ca. 50% of the grains, whereas ca. 40% emit very little to no IRSL. For sample RO1-5, 10% of the grains emit close to 95% of the signal, with 80% of the grains being dim. However, in contrast to Reinmann et al. (2012) we find no relationship between brightness and D_e.

Fig. 7

Light sum curve of single grain data of four samples.

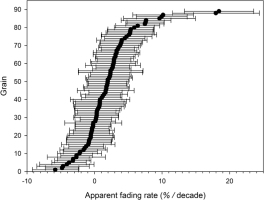
The storage tests carried out on multi-grain samples to estimate the fading rate (Fig. 8) gave g-values between 1.6 ± 0.4 and 2.4 ± 0.3%/decade, overlapping within uncertainties. This represents an average g-value of 2.2 ± 0.2%/decade (standard deviation). For singlegrains, fading rates range from −5.82 ± 3.40 und 18.43 ± 5.12%/decade (Fig. 9). These individual fading rates represent a mean of 1.9%/decade, with a large standard deviation of 4.0 and a standard error of 0.4, overlapping within uncertainties with the values determined for multi-grains. However, negative fading rates are not reasonable considering these describe loss of signal and as there are no obvious mechanisms that could explain the apparent significant signal gain. Of the 89 fading rates determined for single grains, 27 show a negative value (30%). This raises the question if it is necessary to apply individual fading rates for single grains. Trauerstein et al. (2012) suggest to determine individual fading rates, as their average single grain g-values deviate systematically from single aliquot ones. This observation cannot be confirmed in this study where the average single grain and multi-grain aliquot g-values agree well within errors. Furthermore, Rhodes (2015) highlights that measurements of each grain after a delay to assess fading are at the limit of being able to assess whether laboratory fading is shared between grains, or whether it is different for each grain. Applying a Chi-squared (χ²) test to the present data set gives a χ² value of 121 (for n= 89); this would rather imply the presence of a non-Gaussian distribution. However, removing the two highest values (g ca. 18%/decade) results in χ² = 100, hence a value quite close to χ² = n−1, which would indicate a Gaussian distribution. As a consequence, we cannot exclude that the observed spread of individual single grain fading rates is presenting a common mean value that is representative for all grains. Hence, we decided to apply the fading rate determined for multi-grains also to the single grains.

Fig. 8

This example of a fading test displays a g-value of 1.6 ± 0.4 %/decade.

Fig. 9

Result of the single grain fading test.

D_e distributions

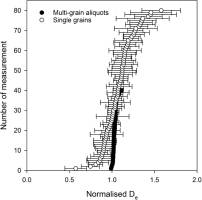
For all four samples we found complex D_e distributions for both single grain and multi-grain aliquots that show a positive skew together with large overdispersion reaching up to 0.79 (Fig. 10, Table 1). Following Bailey and Arnold (2006) and Arnold et al. (2007), this is interpreted as evidence for differential bleaching of IRSL prior to deposition. The spread of multi-grain D_e values is generally smaller than for the single grain approach, and for all samples the lowest values are found for the single grain measurements. The population of lowest D_e values of single grains is up to 50% compared to that of the multi-grains in all samples. In this context it has to be considered that the multi-grain aliquots contain ca. 100 grains of which ca. 10% are rather bright (Fig. 7). Hence, it has to be expected that most of the signal from the multi-grain aliquots origins from a minimum of ca. 10 grains, some of which may have inherited a residual signal. Wallinga (2002) has shown through computer simulations that this will result in averaging effects in the multi-grain analyses that to some extent mask the differential bleaching.

Fig. 10

Dose distributions plots of multi-grain aliquot and single measurements of all samples investigated. Three D_e values of 19.1 ± 1.6 Gy (RO1-5 MG), 11.9 ± 0.4 Gy and 17.2 ± 0.8 Gy (RO1-6 MG) are not shown in the plot to improve presentation.

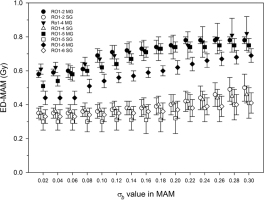
The above mentioned observations call for the appli-cation of the MAM to extract mean D_e estimate from the grains/aliquots presenting the well-bleached fraction. As there is little experience with samples from the region, a sensitivity test was carried out to investigate the effect of the input value σ_b (Fig. 11). The MAM was computed using σ_b values from 0.02 to 0.30, at 0.02 increments. As a matter of fact, the lowest overdispersion reported in the literature for single feldspar grains in natural samples is around 0.15 (Neudorf et al., 2015; Rhodes, 2015) and lower σ_b values are considered to be likely inappropriate input values for the MAM (presented here only for completeness). On the other hand, Neudorf et al. (2015) interpret overdispersion >0.25 to result from partial bleaching, consistent with the value of 0.27 reported by Gaar et al. (2014) for a well-bleached sample. Hence, we use a value of 0.20 as representative of what is reported in the literature as input for the following MAM calculations. Using the extrema of what appears realistic according to literature (0.15, 0.25) would lead to ca. 8% higher or lower values (ca. ten years difference in age for the samples under consideration). For analyses of the multi-grain data set, we used a σ_b of 0.10 following the experiments and modelling of Cunningham et al. (2011).

Fig. 11

Change of D_e when assuming different overdispersion values in the Minimum Age Model of Galbraith et al. (1999).

IRSL ages

IRSL ages have been calculated both without and including fading correction; the difference is about 18% (Table 1, Fig. 12). More obvious is the difference between single grain and multi-grain IRSL ages, the latter being up to twice as old as the first. The multi-grain IRSL ages are between 100–200 years older than the expected age, and this is interpreted to result from averaging effects and masking of partial bleaching as explained above. The single grain IRSL ages, both uncorrected and corrected for fading, fit with the deposition history deduced from historic maps (Fig. 12). According to this, deposition in the lower part of the profile took place around AD 1800, probably just after the thalweg of River Rhine had moved over the area. The upper two samples are by trend slightly younger, with sedimentation ending around AD 1870. This is consistent with dense floodplain vegetation indicated on the historic map of AD 1872 (Fig. 1).

Fig 12

Plot of IRSL ages for different approaches versus the timeline reconstructed from historic records.

5. Conclusions

This study highlights that feldspar IRSL can be used successfully to date very young fluvial sediments, despite the several challenges related to this issue. As averaging effects in multi-grain aliquots mask part of the differential bleaching in the samples, this required application of the single grain approach. The resultant ages are in excellent agreement with the expected deposition history as inferred from the study of old maps. As the offset of the multi-grain aliquot IRSL ages is only 100–200 years, this method may well be suitable for samples being older than a few millennia. Hence, the approach is considered as an alternative in settings where quartz exhibits poor OSL properties. Nevertheless, it is necessary to investigate the effect of thermal transfer, partial bleaching and fading in the samples in more detail, as these have the potential to substantially interfere with accurate calculation of sediment deposition ages.