. Introduction
The stability of luminescence signals stimulated by IR at elevated temperature was first investigated by Thomsen et al. (2008); they found that such signals were significantly more stable than the conventional signal measured at or about room temperature, especially if a room-temperature stimulation preceded the elevated temperature stimulation. Buylaert et al. (2009) tested the application of this new signal to the dating of K-feldspars extracted from sediments; they used a 250°C preheat for 60 s, followed by a 100 s IR stimulation at 50°C and finally a 100 s elevated temperature IR stimulation at 225°C, with blue light detection (320–460 nm); they called this signal post-IR IRSL. Based on studies of the source of the IR stimulated luminescence signal by Murray et al. (2009); Thiel et al. (2011) increased the preheat temperature to 320°C (60 s) and the elevated temperature of stimulation to 290°C (pIRIR290). They applied this revised protocol to samples of Japanese loess, one with age control, and were unable to detect significant signal instability. As a result of these early studies, the feldspar pIRIR signal is now widely used in dating both sand-sized extracts of K-feldspars and polymineral fine-grains (Buylaert et al., 2012).
Although IR dating of ceramics has been used almost since the first identification of the signal by Hürt et al. (1988), such studies either ignored the possibility of anomalous fading or corrected for it by determining fading rates, e.g. Auclair et al.,(2003) and Huntley and Lamothe (2001). Despite the identification of much more stable IR signals from feldspar, few if any studies have tested their application to ceramics (al Khasawneh et al., 2015). Even young heated materials should be well suited to pIRIR protocols, because the high temperature firing should completely empty any IR-sensitive trapped charge (Murray et al., 2009; Thomsen et al, 2011) and eliminate the possibility of thermal transferred signals (Ollerhead et al., 1994); these often limit the applicability to young unheated materials because of the resulting apparent large residual dose, even in well-bleached sediments (Reimann et al., 2011, 2012).
To test the usefulness of such signals, ceramics of broadly agreed age were collected from three superimposed strata from the archaeological site Pella (Tabqat Fahl) in Jordan. The ages of these layers are based on stratigraphy, typology and serration of related finds (see next section). Both IR signals measured at 50°C (IR50) and 290°C (pIRIR290) signals are used in our studies. Routine laboratory tests (recycling ratio, recuperation, and dose recovery), heating and stimulation plateaus are examined to test the reliability of our SAR protocol when applied to the heated fine-grains extracted from the Pella ceramics. The resulting equivalent doses are used to determine luminescence ages for comparison with the known ages, and the results are discussed in terms of the reliability of the IRSL ages.
. Site Description and Independent Age Control
Pella (modern name Tabaqt Fahl) lies in the northwest of Jordan, about 30 km south of Lake Tiberias, 130 km north of the capital Amman, and five km east of the Jordan River. The site lies around sea level, at latitude 32°27’, longitude 35°37’. The settlement is spread across 10 square kilometres, situated in the foothills of the east Jordan valley. A copious water source is located at the base of the southeast corner of the mound, and are well-known hot springs three km north, at Wadi el Hammeh (Fig. 1).
Pella is one of the longest occupied archaeological settlement landscapes in the Jordan Valley. Large-scale excavations on the mound commenced in 1979, as a joint project of the University of Sydney (NSW, Australia), the College of Wooster (Ohio, USA) and the Jordanian Department of Antiquities. Excavations are ongoing with 27 field seasons completed (McNicoll et al., 1992; Bourke, 2014 and Bourke et al., 2006). There are 38 designated excavation Areas, with many other localities explored in less detail across the ruin-field. The largely artificial central settled mound is about 400×250 m in extent, and rises over 30 m high. Settlement on the main mound goes back deep into Neolithic times (ca. 7000 BCE), although the modern tell contours are shaped by 4 m thick mud-brick fortification walls that first surrounded the site in the Middle Bronze Age (ca. 2000–1900 BCE) (Bourke et al., 2006). Across the Wadi Jirm to the south of the main mound, a largely natural hill, Tell Husn, has a more restricted occupational range, stretching from the late Chalcolithic period (ca. 4000 BCE) onwards. Many farmsteads, field-walls and burial grounds dot the landscape surrounding the main mound, for upwards of three km in all directions. (Fig. 1)
Because of its long largely unbroken occupational sequence, Pella is considered a key site in determining the chronology of settled life in the north Jordan valley; the results of 35 years of excavations have shown that occupation has been continuous over the last 12,000 years (Edwards, 2013).
Excavations in more recent times have focussed on the south-central area of the main mound (Area XXXII), where the largest Bronze Age temple ever discovered in Jordan has been under excavation for the past 15 years (Bourke, 2012). More recently attention has shifted to the west of the temple, where a series of Bronze and Iron Age (around 1650–750 BCE) Civic Buildings contemporary with the nearby temple are being uncovered (Bourke, 2011, 2013, 2014).
Since the early 1990s, a program of intensive radiometric sampling has been carried out (Bourke et al., 2006, 2009; Wild and Fischer, 2013), to complement traditional typological methods of establishing relative chronology (McNicoll et al., 1992; Bourke, 2000 and Bourke et al., 2006).
Table 1 lists a selection of 14C ages from the Iron Age destruction horizon from which the OSL samples were collected (Wild and Fischer, 2013)1.
Table 1
Relevant radiocarbon ages for samples from the destruction horizon. The calibration of 14C dates with the calibration software OxCal version 3.10., and the calibration curve lntCal09 (Fischer, 2013)1.
| VERA# (ABA)* | 14C age (BP) | Era and phase | Calibrated 2σ BCE | |
|---|---|---|---|---|
| Pella | VERA 5311 | 2940 ± 35 | IAI-II | 1270–1020 BCE (94%) |
| Pella | VERA 5301 | 2930 ± 35 | IAI-II | 1260–1010 BCE (91%) |
| Pella | VERA 5316 | 2925 ± 35 | IAI-II | 1260–1010 BCE (95%) |
| Pella | VERA 5310 | 2885 ± 35 | IAI-II | 1210–970 BCE (93%) |
1 Vera 5308 and 5316 were processed by Professor Peter Fischer at Vienna in 2011, as part of an SCIEM2000 project on the Iron Age chronology of the Jordan Valley (Wild and Fischer, 2013, 461, n.90). Bourke would like to thank Fischer for making these dates available for discussion here.
In addition, one sample (VERA 5308: 5205 ± 35 BP, 4060–3950 BCE), not shown in Table 1 was taken from a fill layer no more than 30 cm below the horizon sampled for OSL; given the archaeological context (Late Bronze/Early Iron Age), the date was clearly anomalous. Further analysis of this fill deposit revealed a red pebbly clay matrix similar to deposits at the base of the occupational sequence. It contained exclusively sherds and botanical remains drawn from Chalcolithic period horizons. This deposit forms part of the extensive levelling fills carried in to even up the topography in preparation for the construction of the Civic Building, this deposit appears to have been drawn from Chalcolithic period horizons eroding out from the south side of the tell three metres below the Iron Age structure. The proximity of this clay matrix, with its associated Chalcolithic sherds, is important when discussing outliers in the OSL ages (see section 6), particularly given that the mid-body sherds collected for OSL had no typological significance.
. Sampling and Sample Preparation
Sampling
The archaeological materials came from three deposits in Trench XXXIIFF, locus 10.6, locus 15.1 and locus 15.2, all excavated in January 2013 (Bourke, 2013, 2014). All were drawn from thick Iron Age destruction debris layers, which sealed all earlier construction and occupation within the Iron Age Civic Complex. Based on typology, almost all the pottery from this horizon dates from the later Iron I and early Iron IIA periods (ca. 1050–900 BCE).
From each of the loci, around 20 potsherds were collected for luminescence dating (Fig. 2). Because of the destructive nature of this method, we were restricted to using samples of little or no use in any further archaeological study; as a result no meaningful diagnostic studies could be undertaken on these potsherds individually and the associated ages can only come from the ages assigned to the layers as a whole. The samples were taken in January 2013 in such manner as to avoid any direct sunlight exposure.
Figure 2
Potshards were collected from layer 10.6 and the stratigphicaly underlying layers 15.1 and 15.2 (bottom layer) (photograph by S. Bourke).

Any soil attached to the potsherds fragments was kept as a light-protection cover and later used for external dose rate measurement. In addition, ∼ 30 g of soil from each layer was collected directly for dose rate measurement.
Sample preparation and measurement facilities
The potsherds were processed under subdued red light following procedures described in Aitken (1985). Water content measurements were undertaken on each of the fragments before any chemical treatment. After removing around 1 mm of the surface, a double face vice was used to break the fragments and ease the process of crushing with the agate mortar. Two fraction of sand size were extracted; 90–300 μm for coarse grains preparation and <90 μm for fine grains preparation.
For both grain sizes, material was cleaned with 10% of HCl for 3 hours, followed by a overnight rinsing in 10% of H2O2 to remove any organic matter, rinsing in 0.01 N sodium oxalate to separate clay grains; repeated washing was carried out after each step. For coarse grains, samples were treated with 10% HF before separating K-feldspar and quartz using a heavy liquid solution (ρ < 2.58 g/cm3), the quartz-rich fraction was then etched for 40 minutes with 40% of HF to remove the outer alpha-irradiated shell from the grains.
Fine grains in the size 4–11 μm were extracted by applying Stokes’ settling (Frechen et al., 1996), around 1 mg to 3 mg of sample in acetone suspension was settled on 9.7 mm diameter aluminium disks and dried at 50°C.
All luminescence measurements were carried out using Risø TL DA 20 reader, equipped with IR diodes emitting at 875 nm, blue diodes emitting at 470 nm, and a calibrated 90Sr/90Y beta source. Blue-stimulated UV OSL was measured through a U-340 glass filter, and IR-stimulated blue light was measured through a BG-39/7–59 filter combination (Bøtter-Jensen et al., 2003).
Dosimetry
External dose rate: Sediment samples from each layer were collected for gamma dose rate measurement. Radionuclide concentrations were measured using high resolution gamma spectrometry (Murray et al., 1987) and these concentrations were converted into infinite-matrix dry dose rates using the factors given by Guérin et al. (2011), and the assumption that there was (20 ± 10)% escape of 222Rn during burial (this covers all reasonable scenarios). Typical shards are 5 to 10 mm thick; according to Aitken (1985) this will result in an external gamma dose rate to the shard of ∼90% of the infinite matrix dose rate (with a further contribution of ∼ 10% of the internal infinite matrix gamma dose rate), for these potsherds, a typical dose rates in the sediments are similar to those in the shards, and so the error involved is <<5%. The radionuclide concentrations and derived external infinite-matrix dose rates are summarised at the end of Table 4.
Internal beta dose rate: because of the small size of the potshards samples, it was not possible to use gamma spectrometry to determine the internal dose rate. Instead, a Risø low-level gas flow beta multi-counter was used to estimate the total beta activity (Bøtter-Jensen and Mejdahl, 1985, 1988). This approach has the advantage of taking into account any disequilibrium in the U series. About 3 g from each potsherd was ground and mixed with wax (to retain 222Rn) before measurement. We adopted the counting geometry and sample preparation developed by Ankjærgaard and Murray (2007) and compared the observed beta count rates (counts per kilo seconds, cks-1) from Uranium series, Thorium series and 40K standards with the predicted infinite-matrix beta dose rates from the same standards, derived from gamma spectrometry analysis as discussed below.
Two considerations were taken into account before using the conversion factors from Ankjærgaard and Murray (2007). First, they neglected the contribution of beta dose rate from other nuclide contamination in their 238U and 232Th standards. In order to define the beta count rate from each nuclide chain individually, we used the gamma spectrometry analysis of each standard to derive the beta dose rate contribution fraction of 238U, 232Th series and 40K to the total beta dose rate. For the 40K standard 100% of the dose rate was derived from 40K, for 232Th standard, 88.8% was derived from 232Th series, and for the 238U standard, 88.7% was derived from the 238U series. The observed beta count rate from each standard was multiplied by these factors before deriving the conversion factor from beta count to beta dose rate.
In addition, Ankjærgaard and Murray assumed 20% loss of radon when calculating the conversion factor in their U-series calibration; here we make the more correct assumption of full radon retention in these standards (mixed with wax). The revised conversion factors are summarised in Table 2 together with the original conversion factors of Ankjærgaard and Murray (2007).
Table 2
Activities derived from gamma spectrometry for the standards used in Ankjærgaard and Murray (2007) together with a comparison of their conversion factors and those derived here using the modifactions discussed in the text.
CR/β — Count rate/beta dose rate, (Ankjærgaard and Murray, 2007)
MCR/β — Modified Count rate/beta dose rate
CR/α — Count rate/alpha dose rate
In order to test the reliability of the new conversion factors, the beta count rate was measured for the soil samples from Pella site and several other samples that are not related to the current study, the average of the ratio of the predicted beta count rate derived from gamma spectrometry to the observed count rate was 1.02 ± 0.03 (n = 20); this average included 238U and 232Th standards, and the measurement of a composite of 14 potsherds of each layer.
Internal alpha dose rate: Ankjærgaard and Murray (2007) did not consider the possibility of deriving an alpha dose rate from beta counting. We have used the known activity concentrations in their U and Th- series radionuclide standards to derive infinite matrix alpha dose rates (allowing for 232Th contamination in 238U standard and vice versa). The observed beta count rates, after correcting for the real contribution (see above) to beta count rate from each decay series in the standard sample, were divided by these infinite matrix alpha dose rates to give the conversion factors given in Table 2. The observed beta count rate from a shard includes some contribution from 40K, which does not contribute to the alpha dose rate. Rather than assume some global average fractional contribution to beta count rate from 238U and 232Th, we derive a more sample specific conversion factor, excluding the beta count rate contribution of 40K, by estimating the average activity ratios from measurement of the average 238U, 232Th and 40K activities in our shards; these were estimated by combining the beta counting samples of 14 potsherds from each layer into a single gamma spectrometry sample (Table 3). The resulting activities suggest that, in our samples, 45.1 ± 1.6% of the beta counts are derived from the U-series, and 5.5 ± 0.3% from the Thorium-series from Layer L10.6, 54.5 ± 3% from the U-series and 4.5 ± 0.5% from Thorium-series for the middle layer L15.1, and finally the bottom layer L15.2, the fractional contribution from Uranium series was 45.4 ±1.9% and for Thorium series it was 5.4 ± 0.5% (Table 3). On average, the likely beta count rate derived only from the U- and Th-series for each shard were then derived by multiplying the total beta count rates by these fractional contributions, and these predicted beta count rates from the 238U and 232Th- series were converted to alpha dose rates by multiplication by the conversion factors of Table 2, assuming an ‘a’ value of 0.09 ± 0.01 (see Aitken, 1985, appendix K).
Table 3
gamma spectrometry analyses of mixtures of 14 potshards from each layer, and the fractional contribution from each nuclide to beta count rate factors.
Table 4
Derived beta and alpha dose rates using the observed beta count rate from each shard. The gamma dose derived from gamma spectrometry analyses of sediment samples from each layer is given at the end of the table.
A summary of the internal alpha and beta dose rates for the potsherds is given in Table 4.
Water content: to estimate the water attenuation factors, measurements of the field and saturated water contents were undertaken for all soil (for gamma dose rates) and shard (for alpha and beta dose rates) samples. Field water contents were chosen as most closely representing the long-term burial average. Water content corrections used the equations given by Aitken (1985)
The cosmic dose rate contribution was evaluated following Prescott and Stephan (1982) and Prescott and Hutton (1994) taking into account the depth of the samples, and combined with the total external dose for each layer to give the total dose rate (Table 5).
Table 5
Summary of ages and related data for 52 potshards. The samples rejected because of low luminescence intensity (test dose response minus background, T-Bg, < 1000) are identified by italics, and the single underlined sample was rejected because of poor recycling ratio. The 3 outliers discussed in the text are highlighted in grey.
Luminescence Characteristics
The majority of the samples provided few sand-sized grains of K-feldspar and quartz; in the few potsherds that yielded quartz; the quantity was insufficient to prepare enough aliquots for efficient equivalent dose measurement. As a result, all further studies were undertaken using poly-mineral fine grains.
In total, fifteen potsherds from deposit L10.6, nineteen from L15.1, and eighteen potsherds from L15.2 were used for estimation of equivalent dose (De). At least eight aliquots were prepared for each potshard.
A modified single aliquot regenerative dose SAR protocol for K-feldspars (Buylaert et al., 2009) was used to estimate the De; the preheat temperature before any IR stimulation was fixed at 320°C and held for 60 seconds before cooling and subsequent IR stimulation. Two stimulations were used: IR at 50°C for 100 s to remove any unstable signal followed by post IR- IRSL stimulation at 290°C for 100 s. The same parameters were used for measurement of signals induced by the test dose. An illumination step using the IR source for 100 s at 325°C was used at the end of each SAR cycle to reduce the charge transfer after repeated thermal and stimulation treatment (Murray and Wintle, 2003).
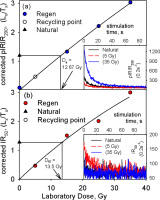
The observed pIRIR290 luminescence signals were relatively weak for most of the samples (Fig. 3) but still stronger than the corresponding IR50 signals. Dose response curves were constructed using integration of the first 20 seconds of the stimulation curves, after subtracting a background based on the final 80 seconds.
Figure 3
Representative dose response curve and (inset) natural and regenerated stimulation curves (a) for post-IR IRSL signals at 290°C and(b) for IR signal at 50°C for shard L15.1.4, from layer L15.1.
The performance of the measured pIRIR290 signal was tested by means of the recycling and recuperation ratios; the average of both values was taken only for aliquots which gave an error <30%. For samples used in age calculations (see section 5 - Equivalent Dose De), 69% of the measured aliquots were accepted following this criterion, and the recycling ratio average is 1.07 ± 0.02 (n = 240). For the average recuperation; 46% of the measured aliquots was used to estimate the average (7.0 ± 0.3% of natural signal, n= 161). Both the recycling and recuperation results are considered acceptable.
De and the first stimulation temperature
The reliability of the dose estimates was first investigated by comparing the pIRIR290 De values integrated after first IR stimulation at various temperatures; samples L10.6.12, L15.1.4 and L15.2.10 were chosen for the measurements. Eighteen aliquots were prepared from each sample, and our SAR protocol applied to groups of 3 aliquots with the first IR stimulation temperature ranging from 50°C to 250°C in 40°C steps. The results are summarised in Fig. 4, and the equivalent dose is considered independent of first stimulation temperature in the temperature region 50 to 210°C, for all three samples. The same variables were applied to the test dose which chosen to be 70% of the expected natural dose (Fig. 4). The ratio between the equivalent doses from the IR signal and pIRIR290 varied between the three samples. For sample L10.6.12 both equivalent doses were similar (mean ratio 0.995 ± 0.042, n = 18). On the other hand, for sample L15.1.4 the De ratio of first IR to pIRIR290 was 0.89 ± 0.04 (n= 18), and the last sample L15.2.10 gave a ratio of only 0.68 ± 0.04 (n=18). The estimates of equivalent doses based on the pIRIR290 appear to be more reproducible for first stimulation temperatures in the region 50–170°C. We chose to use a first stimulation temperature of 50°C in all subsequent measurements because this temperature has been used by others in pIRIR protocols (Buylaert et al., 2012; Thiel et al., 2011) and because almost all previous IRSL measurements on pottery have been made at or close to room temperature.
De and the Preheat temperature
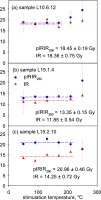
The estimation of equivalent doses was also tested for dependence on preheat temperature. Twenty one aliquots of each of the samples L10.6.12, L15.1.8 and L15.2.13 were prepared; for each sample aliquots were divided into 7 groups of 3 aliquots, and each group was measured using our SAR protocol but with different preheat temperature ranging between 100 and 310°C, increasing by 35°C in each step. The first IR stimulation was fixed at 50°C and the pIRIR stimulation temperature was kept 30°C less than the preheat temperature. The same conditions were fixed for the test dose signal measurement (Fig. 5).
Figure 5
Dependence of De values on the preheat temperature for three representative samples (a) L10.6.12, (b) L15.1.8 and (c) L15.2.13. Red symbols — IR50, blue symbols — pIRIR.
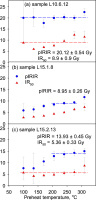
The equivalent dose does not vary significantly over the entire temperature range for sample L10.6.12, for both IR50 and pIRIR signals. For sample L15.2.13, the equivalent doses obtained from the IR50 signal appears not to change significantly over the entire range, but the pIRIR signals are only independent of temperature between 205 and 310°C. On the other hand, sample L15.1.8 behaves differently for the IR50 signals — the IR50 De increases steadily with temperature, although again the pIRIR signals are independent of temperature between 205 and 310°C.
Based on the results of Figs. 4 and 5, we chose to continue measurements using a 320°C preheat and a pIRIR stimulation temperature of 290°C.
Dose Recovery
Finally the overall performance of the chosen measurement protocol was tested using a dose recovery test. Murray (1996) first tested the ability of a regenerative protocol to measure a dose applied before any thermal treatment by giving doses in addition to the natural dose using 60Co gamma irradiation to test his modified SARA protocol. Later Murray and Roberts (1997) exposed different aliquots to daylight prior to dosing. This was justified as an attempt to imitate the natural signal bleaching process for their samples; the approach was later adopted by others (Wallinga et al., 2000). Because the luminescence signals of our samples were initially reset by heat rather than light, we used three approaches to dose recovery tests.
In the first, 3 different samples (L10.6.1, L15.1.3 and L15.2.2) were heated at 500°C for 20 minutes. Aliquots then were prepared and irradiated with about 21 Gy. The ratio of the measured dose to the given was 1.23 ± 0.03 (pIRIR; Fig. 6a.1) and 1.07 ± 0.03 (IR50; Fig. 6a.2).
Figure 6
Ratios of measured equivalent dose to the given dose for both signals in dose recovery measurements: (a) samples heated to 500°C in oven before giving laboratory dose (a. 1 for pIRIR290 signal and a.2 for IR50 signal); (b) samples exposed in solar stimulator for 4 hours before giving laboratory. Note that the IR50 signals were too weak to derive a meaningful dose recovery histogram; (c) samples given laboratory dose in addition to their natural dose, the measured dose to the given dose ratio was calculated after subtracting the natural dose from the total measured dose (c. 1 and c.2 for pIRIR290 and IR50 respectively).
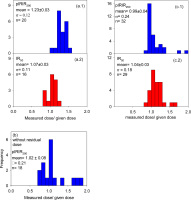
In the second test, 18 aliquots were prepared from each of the same samples and were exposed to light using solar stimulator for 4 hours before giving a laboratory dose of 21.3 Gy. For the same set of samples a further 18 aliquots were prepared and exposed to light for 4 hours, the residual dose was then measured and subtracted from the average dose for each sample from the first set of measurements. After residual subtraction the dose recovery ratio for the pIRIR290 signal was 1.02 ± 0.08 (n = 18; see Fig. 6b).
In the third test, samples were given an additional large beta dose in addition to the natural dose. Thirty two aliquots were prepared from 3 different samples for which the De had been estimated earlier, ∼150 Gy additional beta dose was given to all aliquots before the total dose (given + De) values were estimated. For the pIRIR290 signal, the ratio between the measured and the given dose (after subtracting the measured natural dose from the total measured dose) was in the range 0.75 to 1.35, with average ratio of 0.99 ± 0.04 (n = 32). For the same measurement; the ratio of the measured IR50 dose to the given dose was 1.04 ± 0.03 (n = 29), both ratios are indistinguishable from unity (Figs. 6c.1 and 6c.2).
We conclude that optical bleaching is unable to completely reset the IR signals, but nevertheless we are able to measure a dose accurately after residual subtraction. In addition a dose given in addition to the natural dose was also measured accurately. This latter experiment confirms the ability of our chosen protocol to measure a dose given to our samples before any laboratory optical or thermal treatment.
. Equivalent Doses and Ages
Equivalent Dose De
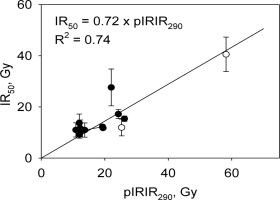
The integration of the signal was for the first 20 seconds of stimulation, and the background was integrated over the last 80 seconds for both IR50 and pIRIR290 signals. One sample (L15.2.13) was rejected because of a poor recycling ratio. In addition, the signals from many shards were very weak; we have chosen to reject all samples for which the average pIRIR290 summed response to the natural test dose was <1000 counts. This resulted in the rejection of 13 shards out of a total of 52 (Table 5). Thomsen et al (2011) have shown that the IR50 signal is significantly less thermally stable than the pIRIR290 signals. Thus if a shard was not heated to a high enough temperature to fully reset the more stable pIRIR290 signal, this should be revealed by an unusually low IR50/pIRIR290 ratio. However the IR50 signals were even weaker than the pIRIR290 signals, and only 3 shards passed the intensity rejection criterion of 1000 counts when the IR50 signals were considered. Even relaxing this criterion to accept IR50 signals >500 counts only accepted 14 shards (out of 52). Fig. 7shows a plot of these few accepted IR50 equivalent doses against the corresponding pIRIR290 equivalent doses and it can be seen that all are consistent with a straight line of slope 0.72 passing through the origin. There is no evidence here for inadequately heated outliers (these would plot significantly below the line) and so we assume that all shards were heated sufficiently to fully empty the IRSL signals.
Although it can be safely assumed that the pIRIR290 signal does not fade significantly (Buylaert et al., 2011; Thomsen et al., 2011), especially at such low doses, we have nevertheless measured fading rates for 3 aliquots each, of two samples, one from layer L15.1 and one from L15.2. The average g2days value measured over 12 hours storage was –1.6 ± 0.4 % per decade (n = 6; data not shown); there is no evidence here for any significant loss of signal confirming our expectations that no fading correction is necessary.
Ages
Age estimates have been derived from the equivalent doses and the total dose rates for a total of 52 samples (Table 5). In Table 5 we list ages with both random and total uncertainties in ages. Random uncertainties arise solely from counting statistics calculated, based on Duller (2007). The total uncertainties include systematic uncertainties arising from external gamma dose rates calculated using gamma spectrometry (common to all shards from a given layer), instrumental uncertainty for Risø OSL reader, beta source calibration (± 2%), water content (± 25%) and Risø Low level beta counter calibration (shared by all samples from the three layers).
We expect, based on archaeological evidence; that the majority of the shards within a layer should be within the same broad age grouping. However it is clear from Table 5 that the random uncertainties in the individual shard ages do not explain the dispersion of the ages from each layer. There are three samples out of the 38 accepted results that are markedly older in age than the remainder (highlighted in Table 5). Two of these outliers were included in the data set of Fig. 7; there is no evidence there for insufficient heating as an explanation for the unusually large equivalent doses of these two samples. In any case, even if these outliers are rejected, the ages within each layer remain over-dispersed. We conclude that our calculated random uncertainties underestimate the true variability in our analyses.
The top half of Table 6 summarise the average age for each layer with the associated standard error, the over dispersion (the degree to which the random uncertainties underestimate the true dispersion) and the total error. The lower part of Table 6 repeats this information but excluding the three outliers discussed above and highlighted in Table 5. This information is repeated for the site average age of 2.85 ± 0.12 ka at the bottom of Table 6.
Table 6
Summary of average ages of each layer and the site average age.
. Discussion and Conclusion
Very few of these samples contained sufficient sand-sized quartz for measurement, and in no cases were there sufficient grains of both quartz and feldspar to allow precise De estimation; as a result all work reported here used polymineral fine grains. Even so, more than 25% of the samples were rejected because of insufficient pI-RIR290 signal, leaving only 38 samples with signals strong enough to be useful. Within each occupation layer, it was anticipated that the majority of the sherds should be from the same period; nevertheless 3 (out of 38) gave ages markedly older than the remainder. However, it is an archaeological commonplace that older materials are often churned up in multi-period ‘tell’ sites such as Pella, which has super positional occupation layers stretching back into the Seventh Millennium BCE.
In the particular case of the Civic Building, the deep foundations of this major structure would certainly have disturbed earlier horizons during the construction process. As well, the large mudbricks used in the construction of the building complex often contained sherds of pottery from much earlier horizons, which were mixed in with the clay when the bricks were made. This resulted in materials from the Bronze Age (~1400 BCE) and the Chalcolithic period (~3200 BCE) being found together with Iron Age materials (~900 BCE) contemporary with the building itself. The 14C sample VERA 5308 (5205 ± 35 cal. years BP, discussed above) drawn from the same Iron Age horizons supports this observation.
We conclude that OSL has successfully identified that three of the sherds expected at the time of excavation to be Iron Age (ca. 1050–900 BCE) are in fact redeposited from earlier occupation potentially as old as the Chalcolithic period (~5000 BCE), probably during the construction of the Civic Building; such limited contamination is completely consistent with archaeological expectations, and does not affect the dating of the occupational horizon, which in all cases is pegged to the latest material in any given deposit.
The typical calculated random uncertainty on each OSL age is ~250 years. From an archaeological perspective, the expected age range per layer is of the order of 50 to 100 years. Thus we would expect analytical uncertainties to dominate the spread in the ages from each layer. However, the age range represented by sherds from the uppermost (yougest) layer is ~1000 years, for the middle layer > 2500 years, and in the oldest bottom layer ~3000 years. It should be noted that the layer with the smallest dispersion (L.10.6, stratigraphically youngest, OD 10%) gives a mean age of 2.72 ± 0.13 ka (random uncertainty), compared with an age of 2.72 ± 0.28 ka for the most dispersed layer (L.15.2, stratigraphically oldest, OD 29%). This suggests that the OD is unlikely to arise from the mixing of older sherds (in addition to those already identified and excluded). We deduce that the considerable over-dispersion in our data is most likely to arise from unidentified laboratory uncertainties. Because of this we cannot meaningfully discuss individual ages of each shard, but only the average age for each layer.
If the three outliers discussed above are ignored, then the three layers have similar average ages, all of which are consistent with the average site age of 2850 years (± 120 years random uncertainty, ± 220 years total uncertainty; Table 6). This average site luminescence age is completely consistent with the expected archaeological age range of between 700 and 900 BCE years (Bourke 2014, which is in good agreement with the relevant 14C ages (Wild and Fischer, 2013), summarised in Table 1, ranging between 970 and 1270 BCE.
In conclusion this study was made more difficult than expected by the absence of sand-sized quartz and feldspars; that, together with the relatively weak signal from poly-mineral fine-grains, gave age uncertainties higher than expected. Nevertheless it has proved possible to identify three samples out of 38 as reworked material. This would have been difficult to demonstrate on typological grounds because these samples did not have marked typological characteristics.
Despite the difficulties in dating these potsherds, we have been able to determine a site age completely consistent with expectation, and this demonstrates the usefulness of pIRIR dating of heated materials from the Jordan Valley. This in turn shows that pIRIR dating can probably be used with confidence on heated materials of unknown age from this region.