Site and samples

The Orkhon Valley was the centre of numerous nomadic states; the Xiongnu (3^rd century BC – 1^st century AD), Turkic (552–745 AD), and Mongol Empires (12^th – 14^th centuries) succeeded one another in the steppes of Mongolia. Archaeological research in Orkhon Valley has concentrated on numerous steles with runic inscriptions, but also on numerous archaeological burials. Khutag Uul Mountains (47°36′N, 102°47′) is located on the left bank of the Khogshin Orkhon River on the eastern edge of the upper Orkhon valley; it was once a tribute to the people of ancient times. The Khutag Uul Cemetery is the largest in its territory. In 2009, during the fieldwork, a total of 121 burial sites were recorded in the south and additionally 43 burials on the east (Bayar et al., 2010), which immediately became the 2^nd Khutag Uul Mountain Cemetery.

The settlement history at this site and the characteristic types of archaeological monuments, especially the sections of burial structures and tombs have been associated with human activities from the Turkic period. However, the graves under study had similar exterior surface structures mounded by an oval or circular stone construction with a diameter of 6–8 m, reflecting a standard tomb of the Xiongnu period. Pottery fragments L-EVA1201 and associated sedimentary samples L-EVA-1202 and L-EVA-1203, L-EVA-1204 from nearby sites ‘MKC 65’ (layer 2) and ‘MKC 4’ (layer 1) were collected taken for single grain measurements (Table S1). The single-grain OSL ages obtained on pottery are compared with single-grain results from sedimentary quartz that revealed post-depositional mixing due to human activities, during the re-using or re-opening of the burial at a later period, which is known to have occurred during the 5^th–6^th century AD (Unpublished Master Thesis Tengis S. 2017)

Sample preparation and measuring facilities

Sample preparation and luminescence measurements were carried out in the Luminescence laboratory at the MPI for evolutionary anthropology, Leipzig (Germany) and followed the standard procedure reported in (Solongo et al., 2019).

Single grains of quartz were measured using a Risø TL-DA-20 reader (Bøtter-Jensen et al., 2003) fitted with a single grain attachment. A 10 mW Nd:YVO₄ solid-state diode-pumped green laser was used for quartz single-grain stimulation, and the signal was detected through Hoya U-340 filters. A 130 mW infrared (IR) diode emitting at 870 ± 40 nm was used for IR depletion test.

D_e determination

To obtain D_e for quartz, the SAR protocol (Murray and Wintle, 2003) was applied to individual grains, which measures the natural signal (L_n), a series of regenerative dose signals (L_x) of 5, 7.8, 12, 15.6, 0 and 5 Gy, and their corresponding test dose signals (T_x). The equivalent dose D_e has been determined using the initial 5–7 channels – signal integrated during the fast decaying part of the OSL decay curve with an appropriate background subtracted. To estimate the decay rates of the fast and medium components, the natural OSL signal (N) and the natural test dose OSL signal (T_n) are fitted to a sum of first-order exponential components using Origin 8.0, running a Levenberg-Marquardt algorithm.

Grains were rejected if the resulting OSL data failed to satisfy the criteria similar to those proposed by (Jacobs et al., 2006), namely if: the relative uncertainty on the first test dose signal T_N was less than three sigma above its corresponding background or its relative standard error is >20%; the recycling ratio is >10%, and the recuperation is >10% of L_N/T_N; (C) the L_N/T_N value exceeded the laboratory-measured dose-response curves; OSL / IRSL depletion ratio differed from unity by more than two sigma and the TL110°C test. To check for the presence of feldspar, an IR depletion-ration test applied to the aliquot was incorporated at the end the SAR sequence (using an IRSL exposure for 100 s at 20°C). The incorporation of TL test to check whether the feldspar component is present involved checking TL whether the range of 150–220°C is at the background level (e.g. Solongo et al., 2019; Hu and Li, 2019).

Quartz OSL characteristics

Quartz pottery single grains

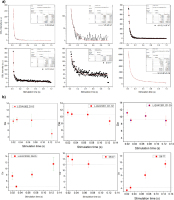
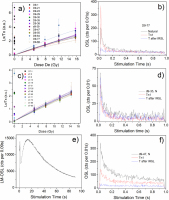
Fig. 1 presents the luminescence characteristics of three representative quartz grains from the pottery sample L-EVA1201. Thermal treatment and annealing of quartz might introduce enhancement in the luminescence sensitivity of annealed quartz (Bøtter-Jensen et al., 1995), and be associated with changes in the defect structures and populations (Poolton et al., 2000) and strong enhancement of the UV emission (Martini et al., 2014). For this quartz L-EVA1201, grain-to-grain variations were negligible. Altogether 300 grains were measured, as expected, the majority of the dose estimates (60%) were accepted and the remaining 120 grains were rejected owing to the lack of an OSL response to the test dose only. The representative natural OSL, test dose OSL and test dose OSL decay curves after IR bleaching at the end of SAR sequence stimulation are shown in Fig. 1b, 1d, 1f. The signal response to IRSL at the end of SAR was negligible confirming that the grains from aliquot are not IR-sensitive; in addition, the presence of the TL 110°C peak further confirms the absence of feldspar. LM-OSL conducted on a single grain identified dominant fast component (Fig. 1c).

Fig. 1

The dose-response curves for individual quartz grains of the heated quartz sample L-EVA1201, showing L_x/T_x as a function of regeneration doses. The corresponding luminescence decay curves from the individual grains are shown on the right side: natural OSL (N – black line), test dose (T₁ – red line and T after IRSL – blue line) OSL decay curves as a function of stimulation time obtained from single grains. In addition, the corresponding TL measured from the aliquot at the end of the SAR protocol served as additional criteria for examining the presence of feldspar.

Fig. 2

a) and c) The dose-response curves for individual quartz grains of the sedimentary quartz L-EVA1202, showing L_x/T_x as a function of regeneration doses. The corresponding luminescence decay curves from the individual grains are shown on the right side: natural OSL (N – blue line), test dose (T₁ – red line and T after IRSL – blue line) OSL decay curves as a function of stimulation time obtained from single grains. In addition, LM-OSL from a bright grain (e) indicated the presence of a significant slow component in addition to the fast component; however those bright grains were rejected.

For each grain, the sensitivity-corrected regenerated OSL signals (L_x/T_x) were fitted with a single saturating-exponential function in the form:

(3.1)

I=Imax[1−eDD0]

where I is the luminescence intensity, I_max is the intensity at saturation, D – dose, and D₀ – the characteristic dose where the intensity I_max is (1–1/exp) times the saturation value. We have obtained values for I_max of 5 to 16 and D₀ values of 24 to 70 Gy. In addition, a global fitting procedure (Fig. 1a) was used to a selection of single grains by fitting a single saturating exponential function; the D₀ values obtained being between 16 and 40 Gy and the equivalent doses between 8 to 12 Gy.

Previously, Roberts and Duller (2004) reported for multi-grain I_max values of 36 to 52 and D₀ values as low as 38.6–55.1 Gy. However, Burbidge et al. (2006) studied younger samples and their values of I_max and D₀ were all lower than those of Roberts and Duller (2004), and they argued that this may because the maximum regenerative dose of 64 Gy was half of that used by Roberts and Duller (2004). In our experiments, the maximum regenerative doses were of 15.6 Gy and 30 Gy, respectively. According to the recommendation of Wintle and Murray (2006), the equivalent dose values of more than 2D₀ should be rejected because of high uncertainty, and the D_e's obtained from SAR and global fitting were less than 2D₀.

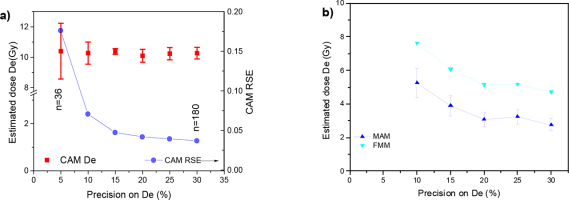
Following this first analysis, we calculated the dose estimates obtained when the relative uncertainty on the natural test dose, and the error in D_e, were less than 30, 20, 15 and 10%, respectively. The effect of the precision on the resultant D_e is shown in Fig. 3a where the estimated dose D_e is plotted against the precision on D_e. As can be seen from the figure, the application of this criterion does not significantly change the CAM D_e (Galbraith and Roberts, 2012) of the distribution. However, the relative spread in D_e values increases as higher precision constraints are applied and results in a significant increase in the relative standard error of 2.7% to 7.5%, as the number of accepted grains meets acceptance criteria decreased from 180 to 65. The over-dispersion OD value reduced from 11.2 to 9.9 ± 0.2%. The most precise estimates (5%) lead to the relative standard error of 15%, which is due to the statistically irrelevant number of grains (n=36).

Fig. 3

Effect of precision on D_e a). for sample L-EVA1201. Central Age Model (CAM, squares) dose and the relative standard error (as circles) on CAM D_e; b). for sample L-EVA1202. FMM and MAM D_e (triangles and squares) as function of precision on D_e.

Presence of an ultrafast quartz OSL component

The addition of the ‘fast ratio’ (Durcan and Duller, 2011) and thus removing the grains with low fast ratios as a criterion for selecting single grains for dose estimation was proposed recently (Duller, 2012); however, it might also lead to the removal of a high proportion of signals (Thomsen et al., 2016). The application of “fast ratio” by calculating the ratio between the fast and medium bleaching components for each grain from both datasets was tested here.

The results of the fitting showed up to three components with decay rates on average of 53 ± 1 s⁻¹, 13.4 ± 0.7 s⁻¹ and 1.2 ± 0.2 s⁻¹. Our results are in agreement with the decay rates of 10.3 ± 3.4 s⁻¹ for the fast and 2.1 ± 0.7 s⁻¹ for the medium components reported by (Feathers and Pagonis, 2015), and of 11 ± 4.3 s⁻¹ and 1.9 ± 1.0 s⁻¹ obtained by (Duller, 2012). We assume that the additional component with the decay rate of 56.6 ± 2.4 s⁻¹ obtained in our measurements may correspond to a very rapidly decaying ultrafast OSL (UF component) in quartz samples, reported earlier for multi-grain OSL by (Jain et al., 2008).

This ultrafast component was identified in samples from different areas around the world, and the optical cross-section of the responsible trap under blue light stimulation is about 14 times larger than that of the fast component (Jain et al., 2008). For dating, the authors suggested removing the UF component by IR bleaching above room temperature, removing by high preheat temperature (>200°C) or rejection of the very initial OSL signal. Interestingly, the preheat did not remove the hypothesised UF component; SAR protocol used in our studies employed preheat at 260°C and cut heat at 220°C, and these preheats are assumed to be high enough to remove the UF component (Jain et al., 2008). This implies that this UF is a) different to Jain et al.'s (2008) and b) that is reasonably thermally stable. Further tests are needed, e.g. high-temperature IR sine IR stimulation at room temperature did not impact the UF. The only evidence that this is a component other than the fast component is the fitting results and the proof of an additional component to the previously reported one.

The initial OSL signal integration interval is assumed to include the fast component preferentially, and rejection of the very initial OSL signal might remove the UF. In the following we examined the effect of variation for the integration intervals on D_e estimation i.e. using the initial part (0.025 s, i.e. channels 6–7) for ultrafast and by rejecting the initial part (integrating 0.03–0.035 s, i.e. channels 7–9) of stimulation to isolate the UF and fast components.

The results are displayed in Fig. 4. We examined the effect of variation for the integration intervals on D_e estimation for pottery L-EVA1201, and for sedimentary quartz LEVA1202 and the corresponding using the D_e-t-plots are shown.

Fig. 4

a) The fitting results for pottery L-EVA1201, and for sedimentary quartz LEVA1202 showing the presence of UF, F and medium OSL components. b) The corresponding constant and increasing D_e-t-plots for L-EVA1201 and L_EVA1202 are shown.

D_e estimates using UF and fast components as radial plots

Comparison of growth curve and radial plots

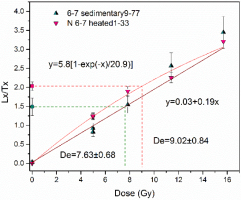
Fig. 5 compares growth curves for pottery L-EVA1201 and sedimentary L-EVA1202. For pottery, the growth curve was fitted by a single saturating exponential function of y=5.8[1–exp /20.9], whereas the sedimentary quartz was fitted using a linear function y=0.03+0.19x.

Fig. 5

Growth curves for naturally sedimentary and heated quartz grains.

Fig. 6a displays a radial plot; the CAM D_e derived from the ‘fast’ and ‘ultrafast’ components were 9.8 ± 0.2 Gy and OD=14.7% which is consistent with the CAM D_e of 9.9 ± 0.1 Gy and OD=15% for UF.

Fig. 6

Radial plots of the single grain dose distributions a) fast D_e from accepted 167 grains (closed triangles) for heated quartz L-EVA1201 and UF D_e from n = 159 (circles). The solid grey band is centered on the weighted mean, D_e determined using Central Age Model, over-dispersion of 14.7%. b) D_e from accepted 134 grains of L-EVA1202 channels 6–9. The solid grey lines indicate the CAM D_e = 15.13 ± 1.47 Gy and overdispersion of 96.8%. MAM D_e = 5.91±1.38 Gy.

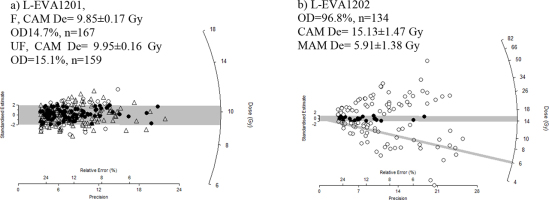
In contrast, Fig. 6b shows radial plot; n=135 out of 500; CAM D_e is 15.1 ± 1.5 Gy with OD=96.8%, suggesting the use of MAM D_e which is 5.9 ± 1.3 Gy.