. Introduction
During the last three decades, passive dosimeters such as CaSO4:Dy, LiF or α-Al2O3:C have been used by numerous luminescence dating groups for measuring environmental (gamma and cosmic) dose rates in the field (e.g., Mejdahl, 1970, 1978; Bailiff, 1982; Valladas, 1982; Kalchgruber and Wagner, 2006; Burbidge and Duller, 2003; Richter et al., 2010). However, due to the rapid development of active systems such as portable γ-ray probes connected to multichannel analysers (e.g., Aitken, 1985; Mercier and Falguères, 2007; Guérin and Mercier, 2011; Arnold et al., 2012), passive systems appear to become progressively abandoned. Indeed, active systems offer the possibility to obtain dosimetric data in a short period (typically, less than one hour) avoiding a second field trip, potentially costly and sometimes even impossible. Nevertheless, during the last years, we have become aware of a new interest in passive dosimeters expressed by groups involved in luminescence and ESR dating. When working at archaeological sites, γ-ray probes (e.g., 2 in × 2 in NaI or larger) usually require rather large holes in the profile wall under study and such damage is not always acceptable at such sites.
Our contribution aims at presenting a straight forward and easy to apply procedure to determine the environmental γ-dose rate using carbon-doped aluminium oxide (α-Al2O3:C) chips as used at the IRAMAT-CRP2A laboratory, Bordeaux (France). We give a description of the used dosimeters, a custom designed field container and the homemade system used for resetting the residual signal in the field. We further present results of Monte-Carlo simulations performed for estimating the fraction of dose absorbed by the aluminium oxide chips in the container in comparison to the infinite matrix dose. Finally, a description of the system and protocol used for measurements is given along with applied correction procedures. Data analysis and correction were developed for and exemplarily carried out using the statistical programming language R (R Development Core Team, 2017) and the ‘Luminescence’ package (Kreutzer et al., 2012, 2017). We complete our contribution with the calibration of the β-source, an estimation of the minimum determination dose with our procedure, a cross-check against reference sites in Clermont-Ferrand, and an application example at the archaeological site of the Sierra de Atapuerca (Spain).
. Dosimeters and field container
The dosimeter choice
Aluminium oxide (α-Al2O3:C; Akselrod et al., 1993) is known to be a highly sensitive dosimeter when its thermoluminescence is measured. It is also known to be light sensitive which enables its stimulation using optical photons (e.g., McKeever et al., 1996) allowing an easy way for resetting the dosimeter, especially in the field. Taking advantage of these physical properties, our group has used α-Al2O3:C for developing a comprehensive dosimetric system easily usable in the field (e.g., archaeological sites).
We use α-Al2O3:C chips produced by Landauer Inc. as detectors. Since its development, this material has been extensively studied (e.g., Whitley and McKeever, 2000; Akselrod et al., 1998; Erfurt et al., 2000) and it is nowadays also used as detector for personal dosimetry (cf. Yukihara and McKeever, 2011). Chips were favoured over powder to avoid, or at least greatly reduce, the risk of contamination in the laboratory while material is handled with various tools (e.g., tweezers, cups, bakers). Moreover, chips which are 5 mm in diameter and 1 mm thick are easy to shape at any step of the procedure.
The field container design
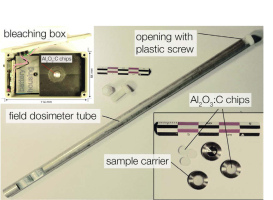
Our chosen container design for depositing the chips in the field considers the demand for small sized housing to limit damages to the site; while at the same time ensuring a full attenuation of ‘natural’ β-particles by the container wall. Taking into account the Monte-Carlo calculations done by Aznar et al. (2003) for different materials and thicknesses and their capacity to stop β-particles, we chose Duralumin as container material. This material has several advantages: it is rich in aluminium and has γ-ray attenuation factors close to aluminium oxide; it is also free of radioelements and easy to handle. Fig. 1 shows a picture of the container consisting of a 27 cm long solid bar of Duralumin with a circular hole with a 5.2 mm diameter at one of its ends. The hole can accommodate three chips and is closed with a rubber O-ring and a nylon screw ensuring water tightness and preventing light exposure of the chips. A technical drawing for custom reproduction is provided in the supplement (Fig. S1).
Fig. 1
Photos of the α-Al2O3:C field equipment. Shown are the homemade bleaching unit (left inset) equipped with a high power blue LED, the chip container (field dosimeter tube), the sample carriers used for luminescence measurements and α-Al2O3:C chips.
Since the container walls absorb a part of the energy carried by γ-rays, the chips do not receive the full infinite matrix dose usually considered in palaeo-dosimetric dating methods. To determine the ratio between the dose (D) and the infinite matrix dose (Dmatrx) the different components of the dosimeter (container, O-ring, screw and chips) have been modelled using the software DosiVox (Martin et al., 2015a). For the computations, the Geant4 (Agostinelli et al., 2003; Allison, 2007) libraries were used (cf. also Martin et al., 2015b). Three different media, for which compositions and densities are listed in Table 1 were simulated: a siliceous sand (hereafter named: Sand), a carbonated sediment rich in clay (CC) and a sediment rich in organic matter (DK). For each medium, a calculation was done independently for the U-series, Th-series and for 40K (Table 2).
Table 1
Composition (in mass %) and densities of the three sediments used for determining the fraction of dose absorbed by the chips, relative to the infinite matrix dose values. Sand: sand sediment; CC: carbonated sediment rich in clay; DK: sediment rich in organic matter.
| Sediment | Density(g cm–3) | Chemical composition |
|---|---|---|
| Sand | 1.8 | SiO2(100%) |
| CC* | 1.8 | O (52.91%), Si (27.71%), Al (8.81%), Fe (7.00%), K (1.55%), Na (0.20%), Mg (0.46%), P (0.11%), S (0.05%), Cl (0.001%), Ca (0.448%), Ti (0.61%), Mn (0.10%) |
| DK** | 1.6 | O (38.30%), C (29.00%), Ca (9.70%), Si (5.40%), Cl (4.10%), P (3.30%), Mg (2.20%), K (1.90%), N (1.20%), F (0.50%), Na (1.90%), Al (1.00%), S (0.70%), Ti (0.10%), Fe (0.70%) |
Table 2
Ratios of the dose (D) absorbed in the Al2O3:C chips to the infinite matrix dose (Dmatrix) for the three sediments: Sand, CC and DK. For calculations, the U- and Th-series were at secular equilibrium.
| Sediment | Series | D/Dmatrix | SE (D/Dmatrix) | Mean | SE(Mean) |
|---|---|---|---|---|---|
| Sand | U-series | 0.938 | 0.061 | 0.931 | 0.052 |
| Th-series | 0.933 | 0.056 | |||
| 40K | 0.921 | 0.040 | |||
| CC* | U-series | 0.921 | 0.071 | 0.938 | 0.041 |
| Th-series | 0.951 | 0.032 | |||
| 40K | 0.940 | 0.021 | |||
| DK** | U-series | 0.938 | 0.040 | 0.939 | 0.041 |
| Th-series | 0.928 | 0.045 | |||
| 40K | 0.951 | 0.038 | |||
The results indicate that, on average, the chips receive a dose which represents 93–94% of the infinite matrix dose (cf. also Martin, 2015).
Signal resetting in the field
Even if α-Al2O3:C dosimeters are fully reset in the laboratory, they are sufficiently sensitive to accumulate a significant signal during travel and need to be reset again in the field. Instead of using a conventional heating system such as a gas torch which requires access to gas cans, we took advantage of the high sensitivity of α-Al2O3:C to light to develop a “bleaching box” (inset Fig. 1, technical drawing Fig. S2). The box houses a blue LED (Luxeon™ –1 Watt Star, 455 nm (FWHM: 20 nm), 100 mW radiometric power, cf. caption Fig. S2 for further details) powered by a standard 9 V block battery. Experiments proved (Fig. S6) that such a simple system allows to reset chips, which had accumulated a dose of a few μGy (a typical travel dose; cf. Bottollier-Depois et al., 2003 for examples) up to a few mGy, within only 2 min (cf. own measurements Fig. S6 and Richter et al., 2010). Nevertheless, it is important to recall that an exposure of α-Al2O3:C to sunlight, and then to UV, might (photo-) transfer charges from deep traps to the OSL trap and then bias the dosimetric measurements (e.g., Burbidge and Duller, 2003). Thus, direct sunlight exposure in the field should be avoided, since it may require a signal resetting at 900°C (or even higher at 950°C; cf. Akselrod et al., 1993).
. Luminescence measurements and source calibration
Equipment and instrumental settings
Luminescence measurements were performed on a Freiberg Instruments lexsyg SMART (Richter et al., 2015). The device is equipped with a 90Sr/90Y β-source (ca. 11 Gy min–1 for coarse grain quartz) and 10 green LEDs (530 ± 20 nm, stimulation spectrum shown in Fig. S3) with a maximum power density of 70 mW cm–2. The green stimulation (GSL, instead of the more classical “blue” stimulation) enables detecting the α-Al2O3:C emission centred at 410 nm (Markey et al., 1995). It should further minimise potential phototransfer of charges from deeper traps into the main OSL trap (cf. Oster et al., 1994, their Fig. 2). The GSL emission was detected through a set of filters (Schott BG3, 3 mm + Semrock 414/46 BrightLine HC interference filter; cf. Fig. S4) placed in front of a Hamamatsu H7360-02 photomultiplier tube (PMT). The channel resolution was set to 0.1 s/channel for OSL. If not stated otherwise, irradiation was performed under the closed shutter (stainless steel, 1 mm; Richter and Kumar, 2014) in front of the β-source using a combination of high-energy electrons and Bremsstrahlung (cf. Bulur and Gösku, 1999; Burbidge and Duller, 2003; Richter et al., 2010, 2015).
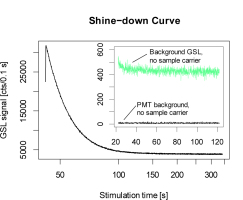
Fig. 2
Typical green stimulated OSL shine-down curve recorded at 70°C with a green stimulation power density of 50 mW cm–2. Before measurement, the chip was heated to 350°C for 10 min and afterwards irradiated for 4 s (ca. 816 μGy) under the closed source. The curve shows a slow decay of the signal, reaching a stable background of ca. 40,000 cts s–1 after ca. 200 s. In contrast, the inset shows a GSL background of the equipment without sample carrier of ca. 6,000 cts s–1 (green curve) and a PMT background (no stimulation) of ca. 100 cts s–1. Background measurement temperature: 70°C.
For the measurements, α-Al2O3:C chips were placed on homemade stainless-steel cups with a circular cavity in their centre (diameter 5.2 mm, depth of 0.2 mm; cf. Fig. 1). This modification holds the chips in the centre of a cup; it also improves the reproducibility of the measurements since the relative positioning of the chips below the irradiation source remains constant. Before the measurements, the sample carriers were heated to 450°C for 10 min in air. The α-Al2O3:C chips were reset at 900°C for 10 min. This pre-procedure applies to all experiments presented below if not stated otherwise.
Measurement sequence
Fig. 2 shows a typical green stimulated (GSL) shine-down curve of an α-Al2O3:C chip previously heated to 350°C and irradiated for 4 s under the closed β-source (ca. 816 μGy; value based on the calibration shown below). The stimulation power density was set to 50 mW cm–2; measurement temperature 70°C (2 K s–1). The luminescence signal decreases slowly and reaches a background of ca. 40,000 cts s–1 after around 200 s. In contrast, the GSL background level of the reader without a sample carrier is an order of magnitude lower (green curve Fig. 2, ca. 6,000 cts s–1; cf. also Fig. S5 for measurements with sample carrier), but still above the PMT background (no sample carrier, no optical stimulation) of ca. 100 cts s–1. We believe that the high GSL background results from diffused photons from the stimulation source through the detection filter set. The initial decay present in all background measurements is likely caused by the stimulation power control in combination with the long OSL lifetimes of α-Al2O3:C which are in order of milliseconds (Markey et al., 1995). Phototransfer from deep traps can be excluded due to the chosen heat treatment prior to all measurements. However, as it will be shown below (Fig. 3), the background including the initial decay was found to be highly reproducible (see also Figs. S5 and S7). Nevertheless, our experiments showed that the background level varies markedly (up to ca. 50%) with the sample carrier used for measurements (Fig. S5, right plot), requiring its precise measurement and aliquot based subtraction during data analysis.
Fig. 3
GSL and TL curves recorded during the reproducibility test. The plot order follows the sequence listed in Table 3 (steps 2,4,5,6). Each plot contains 50 curves. All curves were recorded on one particular sample carrier and α-Al2O3:C chip. The first TL curve (A, red curve) shows that the chip received a small dose after its resetting in an external furnace at 900°C. All particular curves are overlapping, and the signals are highly reproducible.
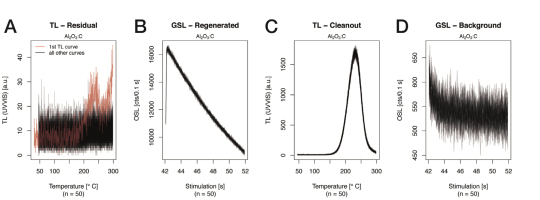
Table 3
Sequence used for determining an accumulated dose in an α-Al2O3:C chip. The LEDs power was set to 50 mW cm–2 and the regenerated dose was 816 μGy. For the three OSL signals, the integration limits were between 0–10 s (0–500 mJ cm–2).
The recommended measurement sequence for dose recovery is listed in Table 3 and consists of only six steps. The sequence takes advantage of the fact that the OSL signal originates predominantly from the peak at 180°C (at ca. 220°C in our system, cf. Fig. S7) and that the dose response is linear over a wide dose range (μGy to Gy; Akselrod et al., 1990). The GSL is stimulated for 10 s only (50 mW cm–2 at 70°C, temperature stabilisation: 20 s) and the remaining signal is depleted by heating to 300°C (steps 2 and 5). The magnitude of the reference dose in step 3 was found to result in a sufficiently high luminescence signal without changing the sensitivity of the samples due to phototransfer. Step 6 records the individual aliquot background. The measurement temperature was set to 70°C to be high enough to avoid unwanted signal contribution from the 35°C (e.g., Markey et al., 1995) TL peak. The chosen stimulation power of 50 mW cm–2, instead of the possible maximum value of 70 mW cm–2, accounts for technical considerations. This value balances the demand for a good signal-to-noise ratio and a reduced ageing of the green LED array. For newer LED arrays with high powered LEDs, higher values might become applicable.
The OSL signals are integrated over the entire 10 s. The background signal is subtracted from the ‘natural’ and reference signals. The recorded TL curves provide a crosscheck only and are not used for data analysis. Assuming a linear dose response, the absorbed dose is determined by using a simple ratio of measured signals and known reference dose.
Reproducibility tests
To test the reliability of the defined measurement protocol (Table 3) and the measurement system, we conducted a reproducibility test. One aliquot (sample carrier and α-Al2O3:C chip) was measured 50 times using the sequence in Table 3. The chip was not irradiated before the measurement. Fig. 3 (A to D) shows the obtained curves of this experiment in the order the curves have been recorded.
Except for the first TL curve (Fig. 3A, red curve, dose received between reset and first measurement), all subsequent curves (TL and GSL) overlap, indicating a high system reproducibility. The dose sensitivity was found to be in the order of ca. 160,000 cts/816 μGy at 70°C. The background curves show a slight signal decay during the first 5 s, which appears to be not dose induced since it was already observed in Fig. 2 (inset, green curve) without a sample carrier. The initial decay seems to be correlated with the activation of the green simulation itself. However, it was found to be highly reproducible and is subtracted as part of the background signal.
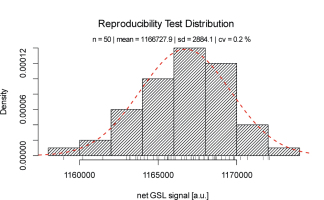
Fig. 4 provides the histogram of the reproducibility test. Amongst the cycle, the material does not suffer from sensitivity changes (cv = 0.2%), justifying the defined simple protocol for routine measurements. This data also indicates that the measurement system is reliable and the use of our modified cups allows for reproducible measurements. Furthermore, following these observations, and considering that the OSL signal of α-Al2O3:C increases linearly with up to, at least, 1 Gy (Akselrod et al., 1990; Markey et al., 1995; Bulur and Göksu, 1997), no particular dose response curve fitting is necessary.
Fig. 4
Stability of the GSL emission over a series of 50 cycles consisting each of a thermal resetting, irradiation for 4 s (ca. 816 μGy), GSL measurement at 70°C, a second resetting and a GSL background measurement. Results are summarised in a histogram. The intensity varies by only 0.2% (cv) reflecting a high system reproducibility.
Irradiation time correction
The high sensitivity of α-Al2O3:C requires special consideration during measurement and data analysis. In a lexsyg SMART an aliquot (sample carrier, chip) is first lifted upward and then moved from the sample carousel into the measurement chamber (i.e. the heating plate). Then the sample arm transports the aliquot to the irradiation position (cf. Richter et al., 2015 for technical details) and back to the heating plate. The whole process takes several seconds. The inertia of the mechanical system introduces further short delays on the order of milliseconds while the sample is directly located underneath the source.
As a result, the sample receives the intended dose (pause beneath the irradiation source) and an additional dose (‘dose uptake’) during the transport in the chamber. The time of the sample transport likely varies from reader to reader. While these effects are small for conventional irradiation with an open shutter, the sample experiences similar dose rates during irradiation under the closed source and during transport in the chamber. Given further the dose sensitivity of α-Al2O3:C, and the required short irradiation times even under a closed shutter, the accumulated dose during the sample transport cannot be ignored. To estimate the ‘dose uptake’ during the sample transport, steps 3–6 (Table 3) were repeated for a chip with increasing irradiation times under the closed source to obtain a dose response. The sequence was repeated five times for the same chip, 12 chips were measured in total.
Fig. S7 (A–C, supplement) shows the obtained GSL and TL curves for one aliquot. The clean out TL curves (Fig. S7B) show a linear growth of the TL signal and with this the luminescence signal of the chip. The background curves (Fig. S7C) further proves that the chosen clean out (TL to 300°C) is sufficient to fully remove the induced luminescence signal on our system.
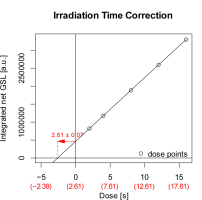
Fig. 5 shows the corresponding linear dose response curve for the five repetitions for one aliquot. Plotted are signals versus intended irradiation times. An intended dose of 0 s results in a significant luminescence signal. To correct for this dose uptake, the curve can be extrapolated to its intercept with the time axis at 2.61 ± 0.07 s. In other words, a pause of 0 s under the closed irradiation source, induces an equivalent dose of ca. 2.61 ± 0.07 s (ca. 533 ± 14 μGy) for the aliquot shown in Fig. 5. The results of all twelve measured aliquots are shown in the supplement (Fig. S8), resulting in a correction value of 2.59 ± 0.02 s (error weighted mean ± standard deviation) for the used equipment. This is, theoretically, the minimum irradiation time possible and consequently the minimum dose that can be delivered by the system (ca. 529 μGy). For practical reasons irradiation times with 0 s are skipped during a sequence, i.e. the sample arm is not moved towards the source and the system continues directly with the next measurement step (pers. comm. manufacturer).
Estimating cumulative dose effects
Routine measurements usually require the analysis of a vast number of chips (each container contains 3 chips). The lexsyg SMART accommodates up to 40 cups on the sample carousel. However, the very compact design of the reader makes unwanted radiation cross-talk effects likely. Such effects are negligible for natural minerals (e.g., quartz), but might become significant for α-Al2O3:C. The longer a chip stays in the sample carousel before its measurement, the higher is the spurious accumulated dose. To estimate the irradiation cross-talk, we prepared a series of 40 α-Al2O3. Chips were heated for 10 min at 900°C in air (rapid cooling to room temperature) before immediately being placed in the sample carousel. To minimise the time between sample loading and the start of the measurement (< 5 s), the sequence was already prepared. The measurement sequence was similar to the one applied for the environmental dose determination (Table 3) to mimic the storage period of the chips in the sample carousel. Samples were measured in numerical order, i.e. sample 1 was measured immediately after loading, while sample 40 was measured after all other samples were completed. The entire experiment (including reset in the external furnace) was repeated three times.
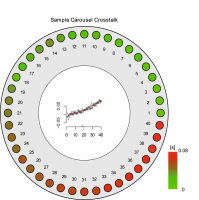
Fig. 6 shows the results of the irradiation cross-talk estimation. The simplified drawing of the sample carousel in the lexsyg SMART shows all 40 sample positions. The colours (from green to red) reflect the average absorbed dose. The inset shows the absorbed dose as a function of position number for all three repetitions of the experiment, a slightly supralinear, but consistent increase of the apparent dose. For one aliquot, an extreme value was observed yielding to a negative dose. Since the α-Al2O3:C chips are not fixed within the sample carrier, we believe that this extreme can be associated with unwanted movements of the α-Al2O3:C chip within the sample carrier after incorrect mounting in the cup. Our results show that such extreme values are seldom (here 1 out of 120 measurements), but possible. Negative values are also observed for other aliquots, in particular for the first positions. To account for this aliquot scatter and to minimise the impact of extreme values we fitted the results using a polynomial function with two variables. The fit is used to correct for the position dependent cumulative dose (cross-talk). Using the procedure listed in Table 3, the cumulative dose for position 40 is below 16 μGy in our system.
Fig. 6
Results of the irradiation cross-talk estimation. The round circle represents the sample carousel with its sample positions. The result for each position is the mean of three measurements, the colours code the equivalent radiation cross-talk in seconds. The inset within the circle shows the individually obtained results for each position. For the irradiation cross-talk correction, the fitted polynomial function (red line) was used. For details see main text.
Radioactive source calibration
To obtain a dose value from the measured OSL signal the irradiation source must be calibrated for Al2O3:C. The lexsyg SMART readers are equipped with 90Sr/90Y β-sources whose activities are usually up to ca. 1.95 GBq, in our case inducing a dose-rate of ca. 0. 18 Gy s–1 in 100–150 μm quartz grains deposited on stainless steel cups.
The resulting dose per second is about 180 times higher than the dose a dosimeter typically accumulates in a year when it is buried in sediment. To reduce the difference between the accumulated natural dose and the dose delivered by the artificial source, dosimeters were placed under the source, while the shutter of the source remained closed. The chip is then irradiated by a mixture of high energy electrons and Bremsstrahlung emission due to the interaction of the β-particles with the material of the shutter (1 mm stainless steel).
To calibrate the β-source α-Al2O3:C chips were exposed to a cubic block (1.2 × 1.2 × 1.2 m) of well characterized bricks (see Richter et al., 2010 for details of the block). The building bricks originate from a single preparation by the manufacturer. A series of randomly selected bricks has been analysed with a high-resolution HPGe γ-ray-spectrometer. The γ-dose rate at the centre of the block was estimated as 1,986 ± 39 μGy a–1 (cf. Richter et al., 2010; infinite matrix assumption, conversion factors: Guérin et al., 2011)1. A cosmic dose contribution of 152 ± 6 μGy a–1 was added considering the location of the block in the basement of the laboratory. The dosimeters (closed Duralumin containers with three chips inside) were exposed within the block for 1,050 days accumulating a dose (γ-dose plus cosmic dose) of 5,801.2 ± 103.5 μGy. The equivalent irradiation time in the lexsyg SMART reader was measured as outlined in Table 3. The dose rate of the built-in source was obtained from the measured irradiation time and the known absorbed dose. In total six chips were measured, one chip was rejected due to a technical error, the final source dose-rate was estimated with 204.12 ± 8.17 μGy s–1 (mean ± standard error, calibration date: 2017-03-31; cf. Fig. S9).
Minimum determination limit
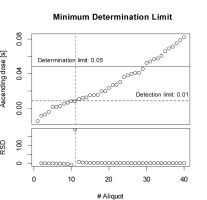
In contrast to instantaneous in situ γ-ray spectrometry, α-Al2O3:C dosimeters require storage in the field from several weeks to months. The shortest possible storage time is determined by the smallest dose that can be measured sufficiently and the onsite dose-rate. Following roughly the suggestions by Currie (1968), we tried to provide an estimate of a meaningful minimum determination limit, i.e. the dose level at which our procedure is believed to provide satisfactory results. Therefore, the measurement results from the irradiation cross-talk estimation (Section 3 – Estimating cumulative dose effects) can be recycled. Before measurement (40 aliquots, three repetitions) all chips have been completely zeroed, thus the dose can be considered as added in discrete steps from ca. 0 μGy up to ca. 16 μGy. Each chip, in combination with the applied procedure, is considered as single detector in its own. In contrast to Currie (1968) absolute dose instead of count values are of relevance. The limit whether a signal (dose) is detected at all is a qualitative decision. Here we define a dose as detected if it is distinguishable from zero (i.e. higher). The ascending dose values in Fig. 7 show that this limit is reached at 0.01 s (ca. 2 μGy). This is the inflexion point in the series of the cumulative relative standard deviation (RSD), which is calculated by sequentially adding dose values and calculate their RSD. For example, the first point reflects the RSD from two dose points, the second point uses three dose points and so on. However, the irradiation time correction measurement has shown a larger scatter between repetitive measurements, yielding a standard deviation out of 12 measurements of 0.02 s. We added twice this value to the decision limit of 0.01, resulting in a minimum determination limit of 0.05 s (ca. 10 μGy).
Fig. 7
Dose values in ascending order, as measured during the irradiation cross-talk estimation (upper plot) and the corresponding cumulative relative standard deviation (RSD, lower plot). Each circle shows the mean for three measurements similar to the values presented in Fig. 6, but in ascending order. The dashed red line indicates the value at which the RSD becomes positive. The black horizontal lines (dashed, solid) indicate the here defined minimum detection level and minimum determination level. For further details see main text.
This value is comparable to the value of 5 μGy reported by McKeever et al. (1996) who used a pulsed optical system for measuring α-Al2O3:C. Assuming an annual y-dose rate of 500 μGy, it would require a storage time of the dosimeter in the field of at least one week. This value does not account for additional inter-aliquot scatter observed in the field (cf. Section 5), but provides an estimate under ideal measurement conditions only to roughly asses the overall procedure performance.
. Data processing
A series of R scripts were developed to allow rapid analysis of the measurement results. These scripts will be released with version (0.8.0) of the R package ‘Luminescence’ (Kreutzer et al., 2012, 2017, early 2018). Prior to release of the new version the functions are accessible via the package development repository on GitHub (https://github.com/R-Lum/Luminescence). Three functions were implemented in the ‘Luminescence’ package that encompass all required steps:
analyse_Al2O3C_ITC() to estimate the irradiation time correction value,
analyse_Al2O3C_CrossTalk() determines the reader specific irradiation cross-talk and finally,
the function analyse_Al2O3C_Measurement() can be used to routinely analyse α-Al2O3:C chip measurements.
The three separate functions allow for flexible workflows. Typically values for the irradiation time correction and the cross-talk are determined once and are only remeasured from time to time. Therefore, the output of the first two functions, i.e. analyse_Al2O3C_ITC() and analyse_Al2O3C_CrossTalk(), can be stored and passed as arguments to the function analyse_Al2O3C_Measurement() for routine measurements, without re-analysing the data for the irradiation time correction and the crosstalk. A complete example workflow using R is provided as, so called, package vignette with the ‘Luminescence’ package (upcoming version 0.8.0) and also before accessible via https://github.com/R-Lum/Luminescence (accessed: 2017-11-24; please follow the instructions on the webpage for the installation of the development version of the package).
. Cross-check and application example
Reference sites cross-check
The developed procedure was tested on independent reference sites. Therefore, we stored twelve α-Al2O3:C chips in four tubes (three each) in four independently analysed references sites (LMP, C341, C347 and PEP) close to Clermont-Ferrand (France). Miallier et al. (2009) describe the sites in detail. The dosimeters were deposited at the locations for 121 days (LMP, PEP) and 144 days (C341, C347) respectively. All dosimeters were shipped back together with previously reset travel dosimeters (four chips in two tubes, one tube per site). For the dosimeter deposition, we used the reference locations (holes in the massive rocks) drilled for the study by Miallier et al., 2009. After arrival, the dosimeters were stored for another three days in a low-level radiation lead castle, before being measured using the above-described procedure.
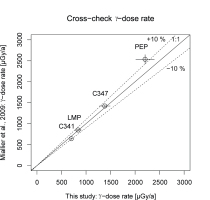
Fig. 8 shows the obtained γ-dose rates plotted against the values published by Miallier et al., 2009 (see also Table S1 numerical results). All results agree within 2σ error ranges, confirming the overall applicability of the proposed procedure. However, the results for the reference site PEP cannot be considered satisfactory. The γ-dose rate measured with the α-Al2O3:C chips, appears to underestimate the value reported by Miallier et al., 2009 by ca. 13%. Local dose-rate inhomogeneity is unlikely to explain the observed discrepancy, and such inhomogeneity was not reported by Miallier et al., 2009. Instead, we found substantial evidence for a movement of the dosimeter tube after its deposition. To minimise corrosion, the dosimeter tubes had been sealed with Gaffer tape (sites: PEP, LMP) or plastic back (sites: C341, C347). The sealing was damaged for the tube at the site PEP, either by an animal or a human. Probably the dosimeter tube was moved partly out of the hole and thus did not receive the full infinite matrix γ-dose. Additionally, we tested all chips used for the cross-check experiment in series of dose recovery experiments (direct measurement and after three days, data not shown), but we found no indication for a particular problem with the chips.
Fig. 8
Gamma-dose rates obtained in this study compared to the values published by Miallier et al. 2009 for four (natural) reference sites. Error bars show 1σ uncertainties. The solid line indicates unity, the dashed lines deviation by 10% from unity. For three out of the four sites the γ-dose rates agree within 10% of unity. However, within 2σ all values are in accordance with each other.
Application example
The full measurement procedure and data analysis was finally applied on dosimeters buried for 258 days in an archaeological site of Sierra de Atapuerca (Spain, Aguirre and Carbonell, 2001; local site: Gran Dolina). Upon arrival, the dosimeters (63 chips, 21 containers, including travel dosimeters, each chips is considered as independent dosimeter) were first stored for a few days in a low-level background lead container. One dosimeter from each of the 21 containers was measured initially. The procedure was then repeated twice more with the second and third dosimeters from each tube.
Irradiation time correction and cross-talk correction values were taken from the measurements described above. The full details of the data analysis, including R code and graphical and numerical output, are provided in the supplementary data (Section 2, supplement). The environmental dose rate (cosmic dose rate and γ-dose rate) recorded by the chips varies between 352 μGy a–1 and 1,315 μGy a–1, with a mean coefficient of variation (cv) of 5.1% (range: 1.1% to 15.1%). The observed scatter is somewhat larger than the scatter reported for the reproducibility tests (Fig. 4B). We observed an inter-aliquot scatter > 5% for 9 out of 21 analysed positions (one position: three aliquots). For 7 out of 63 aliquots, we observed that the TL (step 2 and 4, Table 3) peak position was shifted by > 15 K (cf. figures in Section 2, supplement). Fig. 9A shows the cv per position, red framed circles indicate positions for which a considerable TL peak shift for at least one aliquot was observed (see example in the inset of Fig. 8A). However, neither Fig. 9A nor Fig. 9B (n = 63) show evidence for a correlation of the peak shift with the scatter or the De.
Fig. 9
Coefficient of variation (A) and TL peak shift vs. De (B) for the analysed field dosimeters (n = 63). Please note that in contrast to Section 5 – Application example, De values are given in s instead of Gy, i.e. Cv is not the same. The left plot (A) shows the inter-aliquot scatter (cv up to ca. 18%) for each analysed sample (n = 21). Each circle represents three chips from one sample. Circles with a red coloured frame highlight aliquots for which a significant TL peak shift (cf. inset) was observed. However, the right plot (B, each circle one aliquot, n = 63) shows no correlation between the peak shift and the obtained De. For further details see main text.
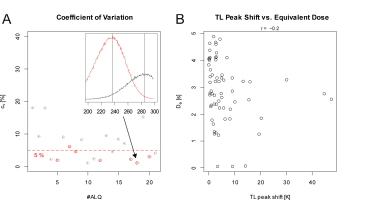
For the final estimation of the environmental γ-dose rate per sample, the individual cosmic dose rate per sample needs to be subtracted from the dose recorded by the dosimeters and finally corrected for dose attenuation caused by the containers (typical for the site described here: 1.065; cf. Section 2 – The field container design).
. Discussion
Our contribution presents a comprehensive system and workflow to estimate the environmental γ-dose rate using α-Al2O3:C chips as passive dosimeters. Such application is not new and its general suitability for estimating environmental γ-dose rates has been reported previously by, e.g., Kalchgruber, 2002 (also β-dose estimation), Burbidge and Duller, 2003 or Richter et al., 2010. However, here, for the first time we presented a complete and easy to apply workflow including the development of open-source software to analyse the results in a transparent and reproducible way using GSL and a lexsyg SMART system. The applied protocol consists of only six steps (Table 3). This minimises the needed measurement time and reduces radiation cross-talk in the reader to a minimum. The protocol comprises very short (10 s) OSL stimulation times and does not require measurement of a dose response curve or test dose correction. The background shows 40,000 cts s–1 after ca. 200 s (green LED, 50 mW cm–2), probably resulting from a diffusion of photons from the green LED array. Both, the short protocol without a test dose correction and the high background might constrain the practical applicable dose range of the protocol. However, we found that the signal reproducibility of 0.2% (Fig. 4B), which is slightly better than the value of 0.7% reported by Burbidge and Duller, (2003,) justifies the chosen protocol. The estimated minimum determination level of ca. 10 μGy suggests that the high background is not an issue; though it can be potentially reduced in the future by pulsing. By contrast, the observed inter-aliquot scatter (mean cv = 5.1%) is significantly higher than the value obtained for the signal reproducibility (0.2%) and may be considered as the main source of uncertainty in the dose evaluation. The precise reasons for the scatter are unknown, since we found no evidence for particular problems with the chips. However, we believe that it is caused by a combination of the real dose scatter recorded by the chips (e.g., differently distributed cosmic-dose rate due to the horizontal storage of the chips) in combination with the measurement system (sample carriers, slightly differing geometric shape of the chips). Burbidge and Duller (2003) obtained a similar value for simulated repeated field deployments (5.4%). Future experiments are needed to address this issue in more detail. In the meantime, confidence in the results can be improved by depositing more dosimeters (tubes) in the field, e.g., two tubes instead of one per sampling location.
We showed that the high sensitivity of the dosimeters requires an irradiation time correction of 2.6 s (ca. 531 μGy), a value that must be determined for each reader individually. Burbidge and Duller (2003) reported a value of only 9.5 μGy (called ‘zero dose’) for their Risø TL/OSL DA-10. This difference is not surprising considering the different instrument design resulting in a closed-source dose rate of ca. 0.69 μGy (Burbidge and Duller, 2003) vs. ca. 204 μGy (this manuscript). However, in contrast to Burbidge and Duller (2003) our approach supports the loading of multiple aliquots at the same time (Burbidge and Duller, 2003, p. 286: “[…] practical to analyse only one chip at a time.”)
It should be further mentioned that there is no reason to believe that an irradiation time correction is only needed for α-Al2O3:C chip measurements. If the dose rate in vicinity of the source is similar to the dose rate used during irradiation, typical for irradiations using Bremsstrahlung (closed shutter), such measurements may also benefit from the irradiation time correction reported above to avoid systematic errors.
Our procedure is tailored to suite the capabilities of a lexsyg SMART reader. However, the general procedure should be applicable on every other luminescence reader equipped with green LEDs with sufficient power density (we recommend a minimum of 50 mW cm–2). The number of aliquots placed within the reader should to be adapted for each system, to minimize the time spent by single dosimeters in the vicinity of the source.
. Summary and conclusions
We presented an easy to use system and workflow, allowing for environmental dosimetric measurements. The system can be applied to geological and archaeological sites if the situation allows storage of the used dosimeter tubes over a couple of months (depending on the environmental dose rate). In the presented procedure we used three chips per container and only one container per sampling position. This approach is sufficient for profiles with many sampling positions. However, with regard to the observed inter-aliquot scatter it might be useful to deposit more than one field container at a location, to gain a higher precision, if needed. Furthermore, we summarise:
– Our system consists of a Duralumin tube accommodating three α-Al2O3:C chips (5 mm in diameter, 1 mm thick each, Landauer Inc.). The container was specifically designed for sites where damages by dosimetric measurements must be minimised (e.g., archaeological and historical sites),
– Monte-Carlo simulations using Geant4 allowed to assess the fraction of dose recorded by the chips in comparison to the infinite matrix dose, in three typical environments (a carbonated clay, a siliceous sand and an organic rich sediment),
– residual signals are reset in the field with a homemade bleaching box,
– the α-Al2O3:C chips are measured with a lexsyg SMART device from Freiberg Instruments using a six-step measurement protocol,
– we revealed the need for a correction of the irradiation time by ca. 2.6 s to allow for additional radiation exposure during storage and transport in the measurement chamber,
– our experiments showed the high reproducibility of the measurement system and the low cumulative dose effects when 40 cups are loaded at the same time in the device (< 16 μGy),
– the minimum (meaningful) dose that can be determined was estimated at ca. 10 μGy,
– the dose of each chip was finally analysed using customised R code, which will be part of the upcoming release of the R package ‘Luminescence’ (version 0.8.0, early 2018),
– our data processing is tailored to a lexsyg SMART reader. Nevertheless, the procedure should be applicable to any other luminescence reader.
We finally argued that any change in the system geometry or setting (including firmware updates) might require a re-evaluation of the values used for correcting the irradiation time and of estimating the irradiation cross-talk. Future work will test the hypothesis whether the inter-aliquot scatter is caused by cosmic-rays.