. Introduction
Radiocarbon is a radioactive isotope of carbon with a half-life 5730 years; it is a cosmogenic radionuclide, produced in the upper layer of atmosphere by the reaction of cosmic rays with nitrogen (14N) nuclei (Godwin, 1962; Lal and Peters, 1967; Burchuladze et al., 1980). Together with other isotopes (13C and 12C), 14C enters the biological and geochemical carbon cycles, and will be assimilated by all living organisms, in which equilibrium between decay and its replenishment is established (Bronić et al., 2010). After death, the exchange between atmosphere and organisms stops and the 14C content assimilated will decrease due to radioactive decay. The radiocarbon method gained a great interest during the last decades, due to its wide applications, such as archaeology (Olsen et al., 2013), forensic studies (Marzaioli et al., 2011), hydrology (Hoque and Burgess, 2012; Nakata et al., 2013), geology and recently ecology and environmental studies as reported by Battipaglia et al., 2010 and Rakowski et al., 2013. Hence, it was important for Lebanon to create a radiocarbon laboratory dedicated to undertake similar research.
The radiocarbon laboratory at the Lebanese Atomic Energy Commission applies the conventional radiocarbon method, based on benzene synthesis and measurement by liquid scintillation counter. It is a standard method issued by the American Society for Testing and Materials in 2011 with a code ASTM-D 6866-11 Method C (Edler, 2009; ASTM, 2011). Optimization was carried out to test the effectiveness of the lab through the analysis of a set of reference materials and left over proficiency test samples. As well as calibration, normalization of the measurement system was applied, counting regions were set for both Teflon and glass vials and stability of standards used was tested (Baydoun et al., 2014).
The method validation is applied in analytical laboratories as an essential part of quality assurance system (Ahmad et al., 2007) and as a basic technical requirement of ISO 17025 standard for testing and calibrating laboratories (Taverniers et al., 2004; Thompson et al., 2002), especially those interested to be accredited. It makes use of a set of tests that demonstrate whether the method is appropriate for its intended use (Magnusson and Ornemark, 2014) as well as to prove the qualification, performance and competency. Internal method validation was expressed in terms of trueness, repeatability (within run precision), reproducibility (between run precision), limit of detection, minimum detectable activity and combined uncertainty calculation.
As our radiocarbon laboratory is interested to study the impact of human activities on the ecosystem using the radiocarbon content in tree leaves as pollution biomarker, it was important to validate the method used to demonstrate that the procedure, when correctly applied, produces results that are fit for purpose. As wood, tree leaves and grass follows the same working procedure, a representative reference wood sample was used for internal validation.
. Methods
Samples
For internal method validation, a reference wood sample, IAEA-C5 (Różański et al., 1992) with a Fraction Modern F14C = 0.2305 ± 0.0002, was used. While for quality control, samples used were Barley (D) from the Sixth International Radiocarbon Inter-comparison (SIRI), humic acid (U) and murex shell (R) from the Fifth International Radiocarbon Inter-comparison (VIRI), Travertine IAEA C-2 and oxalic acid IAEA C-7. Reference values are presented in Table 5. All reference samples were dried at 105°C without any previous chemical treatment (Różański et al., 1992; Baydoun et al., 2014).
Benzene synthesis
Conventional method for benzene synthesis was used (Barker, 1953; Tamers, 1975). This method was widely applied in large number of laboratories and by many scientists (Beramendi-Orosco et al., 2006; Mazeika et al., 2008). The standard method consists of the following essential steps (Edler, 2009; ASTM, 2011): 1) lithium carbide production, 2) acetylene production, 3) trimerization of acetylene to transform it to benzene. 3 g of the reference sample were poured into a titanium liner which was then inserted into a stainless-steel reactor containing metallic lithium. The reactor was then closed, evacuated, and heated in an electrical furnace at 750°C. The obtained lithium carbide was then converted to acetylene (C2H2) by vacuum hydrolysis, purified by passing through a chromic acid solution and captured in a vial immersed in liquid nitrogen. The produced (C2H2) was unfrozen and transformed to benzene (C6H6) using vanadium catalyst previously regenerated at 300–400°C. The benzene was purified by sulphuric acid followed by sublimation (Muraki et al., 2001). Butyl-PBD was used as scintillator in proportion of 10 mg per 1 g of benzene.
Measurements
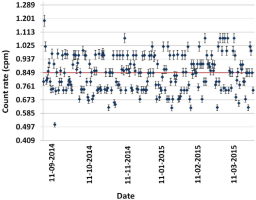
Low level liquid scintillation counter, Tri-Carb 3180 TR/SL (QuantaSmart, 2008) was used for radiocarbon measurement. Background, C-14 and H-3 traceable standards of known activities provided by Perkin Elmer were used to carry out normalization that is a part of Instrument Performance Assessment (IPA). This is applied on routine basis (L’Annunziata and Kessler, 2012). Normalization is carried out periodically in order to assess the performance and stability of the measurement system. Standards were counted in 20 consecutive cycles for 20 seconds each (QuantaSmart, 2008). The IPA data and reports are generated automatically by the LSC (QuantaSmart, 2008; L’Annunziata and Kessler, 2012). The main parameters that are checked are the efficiency and background in the carbon and tritium window. Fig. 1 represents the detector background stability over time. The data presented are obtained from weekly measurements made on the same weekday over the period of six months. The counting region optimization was performed to maximize the figure of merit (FOM = E2/B) which was calculated at three counting windows where E is the efficiency and B is the background count rate of the blank (Bronić et al., 2009; Baydoun et al., 2014). For this purpose, blank sample containing 4 g commercial dead benzene and a standard sample were measured in the adopted counting geometry (4 g benzene). The standard is radioactive benzene of known activity to which Butyl-PBD and dead benzene are added to fix the counting geometry (4 g). All related data were presented in Table 1. Quenching correction was not taken into consideration in our work as the counting geometry of the standard and sample is the same. The tested samples were counted in 6 cycles for 300 minutes resulting in total of 1800 minutes per sample. 20 ml low potassium glass vials from Perkin Elmer were used. The results are reported as F14C which was obtained from the ratio of specific activity of sample to that of the standard used (Reimer et al., 2004).
Internal method validation
The purpose of the validation is to verify that the conventional radiocarbon method, used for the determination of radiocarbon content in tree leaves, grass and wood, when applied in our laboratory, fits to its intended use.
Trueness
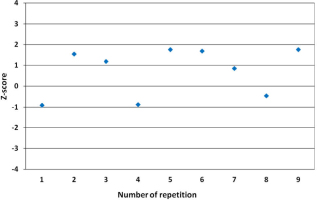
Trueness was used to test the closeness of analytical result to the reference value and it was quantified in terms of bias (Taverniers et al., 2004). As well as, a statistical parameter, z-score was used to test the acceptance of the results. The whole working procedure consisting of benzene synthesis, measurement and calculation was applied to the reference sample at 10 duplicates. The bias was calculated according to Eq. 2.1 (Magnusson and Ornemark, 2014), Xref is the reference value; X is the mean value of the duplicates. The calculation of z-score is described by Eq. 2.2, where XLab and σLab are the laboratory value and its quoted uncertainty respectively. Values lying between –2 and for +2 are considered to comply with fitness for purpose, while values outwith –3 or +3 are unusual and would need further investigation (Scott et al., 2010; Sironić et al., 2013).
Precision
The precision parameter was applied to test the closeness of independent test results under stipulated conditions (Thompson et al., 2002; Taverniers et al., 2004; Scott et al., 2007). It was expressed in terms of repeatability (within run precision) and reproducibility (between run precision). Eq. 2.3 and Eq. 2.4 were used to calculate repeatability limit (r) and reproducibility limit (R).
Where t∞ is the Student’s two tailed value (1.96) for a Confidence Level of 95%, and degree of freedom ∞, σr and σR are respectively the standard deviations of the observed values under repeatability and reproducibility conditions.
The precision was then evaluated based on the coefficient of variation (CV) calculated according to Eq. 2.5 and compared with the tolerance 5% stated in the method (ASTM, 2011). Where σ is the standard deviation of the repeated measurements under repeatability and reproducibility conditions.
For repeatability, benzene synthesis from the reference sample was carried out ten consecutive times, and then, the obtained benzene replicates were counted under identical measurement conditions using the same measured standard and the same background. While for reproducibility, four replicates were prepared and counted with one parameter change (Magnusson and Ornemark, 2014). The changed conditions are the background or blank sample in calculation, count rate of the standard, the scintillator and the counting time from 300 minutes to 150 minutes.
Minimum detection limit and minimum detectable activity
The smallest true net signal that can be reliably detected was expressed in terms of minimum limit of detection (LD) where the minimum detectable activity (MDA) is the smallest activity that can be detected with a predetermined probability. Both LD and MDA were calculated according to Currie Formula (L’Annunziata, 2003; Herranz et al., 2008) as follows
Where B is the total count of blank sample counted for the same counting time as the sample. The factor 4.65 is derived from statistics and accounts for a 95% confidence level (Passo and Cook, 1994). Ten sample blanks containing dead benzene and scintillator were prepared; the average value was used to calculate the limit of detection (LD). LD and MDA were expressed in counts and dpm respectively. Eff is the efficiency and T is the counting time in minutes.
Uncertainty Calculation
The Fraction Modern (F14C) was calculated according to Eq. 2.8, where As and Astd are respectively the specific activities (cpm/g C) (Canducci et al., 2013) of the sample and the standard measured in the same year.
The main sources of uncertainty that were taken in consideration in this work were the count rates of the sample, standard and background, as well as the mass of standard and the sample. The combined relative standard uncertainty of the Fraction Modern was calculated according to “propagation law” (GUM, 1995; Scott et al., 2007) as shown in Eq. 2.9, it is the square root of the sum of the square of the individual relative standard uncertainties.
However, partial uncertainty for quenching correction was considered negligible as the counting geometry of standard and sample is the same. In case of age or Δ14C calculation, one should include standard relative uncertainty of isotope fractionation for δ13C and the half-life of 14C.
Quality Control Procedure
Another tool for internal validation and for checking the reliability of results is the application of a quality control procedure based on the benzene synthesis and measurement of reference samples representing different matrices. For this purpose, travertine IAEA C-2, oxalic acid IAEA C-7, barley (D) from the Sixth International Radiocarbon Inter-comparison (SIRI), humic acid (U) and murex shell (R) from the Fifth International Radiocarbon Inter-comparison (VIRI), were analyzed. Results are evaluated based on z-score values. Data are presented in Table 5.
. Results
The ten replicates values of F14C, under repeatability conditions were presented in Table 2. Values ranged between 0.22 and 0.24 with a mean value of 0.23. This mean value was used to evaluate the bias, which was found to be 1.51% and hence it was appropriate value as being lower than the acceptable tolerance level 5% stated in the method (ASTM, 2011). For reproducibility, the four replicates F14C values, presented in Table 3, varied between 0.23 and 0.24 with a mean value of 0.24. The data of internal validation for the determination of Fraction Modern were represented in Table 4. The coefficients of variation for evaluating the precision were found to be 2.70% and 3.30% under repeatability and reproducibility conditions respectively. Values lower than the tolerance level of the method, and as consequence data were acceptable. The calculated z-score values, for all reported F14C were presented in Fig. 2, they found to lie between –2 and for +2, and then they complied with the acceptance criteria. The calculated combined uncertainty was found to be in the order of 2.58%, a value comparable to the stated uncertainty of the method 3%. Table 5 represents the results obtained from the analysis of five different reference samples, z-score values were found to range from –0.96 to 0.90 and as consequence data were acceptable.
Table 2
The ten Fraction Modern (F14C) values obtained under repeatability condition.
| Number of repetition | Value of F14C |
|---|---|
| 1 | 0.224 ± 0.006 |
| 2 | 0.241 ± 0.007 |
| 3 | 0.237 ± 0.006 |
| 4 | 0.225 ± 0.006 |
| 5 | 0.242 ± 0.007 |
| 6 | 0.230 ± 0.006 |
| 7 | 0.236 ± 0.006 |
| 8 | 0.240 ± 0.007 |
| 9 | 0.230 ± 0.006 |
| 10 | 0.231 ± 0.006 |
Table 3
The four Fraction Modern (F14C) values obtained under reproducibility condition.
| Number of repetition | Value of F14C |
|---|---|
| 1 | 0.244 ± 0.008 |
| 2 | 0.235 ± 0.006 |
| 3 | 0.227 ± 0.006 |
| 4 | 0.242 ± 0.007 |
Table 4
Validation parameters for the determination of Fraction Modern (F14C) by conventional method when counting 4g benzene for 300 minutes.
| Validation parameters | Value | |
|---|---|---|
| Method Bias | 1.51% | |
| Repeatability | Mean* | 0.23* |
| σr | 0.01 | |
| rL | 0.02 | |
| CV | 2.70% | |
| Reproducibility | Mean | 0.24 |
| σr | 0.01 | |
| RL | 0.02 | |
| CV | 3.30% | |
| Limit of detection | Ld (counts) | 2.98 |
| Minimum Detectable Activity | MDA (dpm) | 0.003 |
| Combined uncertainty | U(pMC) | 0.58 |
Table 5
Reference values, Lab values and z-score values.
| Sample Code | Sample type | Reference value (F14C)* | σtarget | Lab Value (F14C) | σLab | z-score | tSIE** |
|---|---|---|---|---|---|---|---|
| D | Barley | 0.1030 | 0.0100 | 0.1038 | 0.0210 | 0.04 | 682 |
| U | Humic acid | 0.2308 | 0.0002 | 0.2298 | 0.0083 | –0.12 | 683 |
| R | Murex shell | 0.7334 | 0.0004 | 0.7210 | 0.0176 | –0.70 | 685 |
| IAEA-C2 | Travertine | 0.4114 | 0.0003 | 0.4217 | 0.0114 | 0.90 | 682 |
| IAEA-C7 | Oxalic acid | 0.4935 | 0.0012 | 0.4810 | 0.0130 | –0.96 | 680 |